Thử tài bạn trang 104 Tài liệu dạy – học Toán 7 tập 2
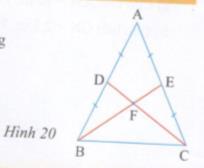
Giải bài tập Cho tam giác ABC cân tại A (hình 20) có BE và CD là hai đường trung tuyến cắt nhau tại F. Biết BE = 9 cm.
Đề bài
Cho tam giác ABC cân tại A (hình 20) có BE và CD là hai đường trung tuyến cắt nhau tại F. Biết BE = 9 cm.
Tính độ dài đoạn thẳng DF.
Lời giải chi tiết
∆ABC cân tại A (gt) => AB = AC.
∆ABC có BE, CD là hai đường trung tuyến cắt nhau tại F (gt)
=> E, D lần lượt là trung điểm của AC, AB và F là trọng tâm của tam giác ABC
Do đó \(AE = {1 \over 2}AC,AD = {1 \over 2}AB,CF = {2 \over 3}CD.\)
Xét ∆ABE và ∆ACD có: AB = AC, \(\widehat {BAE}\) (chung)
AE = AD (\(AE = {1 \over 2}AC = {1 \over 2}AB = AD\))
Do đó ∆ABE = ∆ACD (c.g.c) => BE = CD. Nên CD = 9cm
Ta có \(CF = {2 \over 3}CD = {2 \over 3}.9 = 6(cm)\)
Mà CF + DF = CD (F nằm giữa C, D)
6 + DF = 9 => DF = 9 – 6 = 3 (cm).