Trắc nghiệm Bài 68: Đề-xi-mét vuông Toán 4 Cánh diều
Đề bài

Đề-xi-mét vuông được kí hiệu là:
A. \(c{m^2}\)
B. \(d{m^2}\)
C. \({m^2}\)
D. \(m{m^2}\)

Điền số thích hợp vào ô trống:
\(3 d{m^2} =\)
\(\,c{m^2}\)

Điền số thích hợp vào ô trống:
\(12{m^2} =\)
\(d{m^2}\)

Điền số thích hợp vào ô trống:
\(4000c{m^2} =\)
\( \,d{m^2}\)

\(1890{m^2}\) được đọc là:
A. Một nghìn tám trăm chín chục mét vuông.
B. Một nghìn tám chín mươi mét vuông.
C. Một nghìn tám trăm chín không mét vuông.
D. Một nghìn tám trăm chín mươi mét vuông

Điền số thích hợp vào ô trống:
Ba mươi hai nghìn chín trăm sáu mươi lăm đề-xi-mét vuông viết là
\(\,\,d{m^2}\).

\(7{m^2}\,4d{m^2} = \,...\,d{m^2}\).
Số thích hợp điền vào chỗ chấm là:
A. \(74\)
B. \(704\)
C. \(740\)
D. \(7004\)

Điền dấu (\(>; <; =\)) thích hợp vào ô trống:
\(2002c{m^2}\,\,\)
\(\,\,20d{m^2}\,20c{m^2}\)
Cho hình chữ nhật có kích thước như hình vẽ dưới đây:
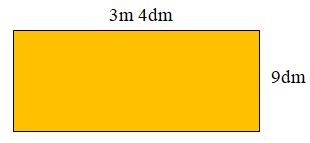
Diện tích hình chữ nhật đó là:
A. \(306d{m^2}\)
B. \(316d{m^2}\)
C. \(306{m^2}\)
D. \(316{m^2}\)

Cho hình vuông ABCD có $AB = 6m$. Hỏi diện tích hình vuông ABCD bằng bao nhiêu đề-xi-mét vuông?
A. \(36d{m^2}\)
B. \(360d{m^2}\)
C. \(3600d{m^2}\)
D. \(36000d{m^2}\)
Lời giải và đáp án

Đề-xi-mét vuông được kí hiệu là:
A. \(c{m^2}\)
B. \(d{m^2}\)
C. \({m^2}\)
D. \(m{m^2}\)
B. \(d{m^2}\)
Đề-xi-mét vuông được kí hiệu là \(d{m^2}\) .

Điền số thích hợp vào ô trống:
\(3 d{m^2} =\)
\(\,c{m^2}\)
\(3 d{m^2} =\)
\(\,c{m^2}\)
Dựa vào tính chất: \(1d{m^2} = 100c{m^2}\)
Ta có: \(1d{m^2} = 100c{m^2}\)
Nên \(3d{m^2} = 300\,c{m^2}\) Vậy đáp án đúng điền vào ô trống là \(300\).

Điền số thích hợp vào ô trống:
\(12{m^2} =\)
\(d{m^2}\)
\(12{m^2} =\)
\(d{m^2}\)
Dựa vào tính chất: \(1{m^2} = 100d{m^2}\).
Ta có: \(1{m^2} = 100d{m^2}\)
Nên \(12{m^2} = 1200d{m^2}\) Vậy đáp án đúng điền vào ô trống là \(1200\).

Điền số thích hợp vào ô trống:
\(4000c{m^2} =\)
\( \,d{m^2}\)
\(4000c{m^2} =\)
\( \,d{m^2}\)
Dựa vào tính chất: \(1d{m^2} = 100c{m^2}\).
Ta có: \(1d{m^2} = 100c{m^2}\)
Nhẩm: \(4000:100 = 40\)
Do đó \(4000c{m^2} = 40d{m^2}\) Vậy đáp án đúng điền vào ô trống là \(40\).

\(1890{m^2}\) được đọc là:
A. Một nghìn tám trăm chín chục mét vuông.
B. Một nghìn tám chín mươi mét vuông.
C. Một nghìn tám trăm chín không mét vuông.
D. Một nghìn tám trăm chín mươi mét vuông
D. Một nghìn tám trăm chín mươi mét vuông
Đọc số đo diện tích trước rồi đọc tên đơn vị đo diện tích sau.
\(1890{m^2}\) đọc là một nghìn tám trăm chín mươi mét vuông.

Điền số thích hợp vào ô trống:
Ba mươi hai nghìn chín trăm sáu mươi lăm đề-xi-mét vuông viết là
\(\,\,d{m^2}\).
Ba mươi hai nghìn chín trăm sáu mươi lăm đề-xi-mét vuông viết là
\(\,\,d{m^2}\).
Viết số đo diện tích trước rồi viết tên đơn vị đo diện tích sau.
Ba mươi hai nghìn chín trăm sáu mươi lăm đề-xi-mét vuông viết là \(32965\,\,d{m^2}\).
Vậy số thích hợp điền vào ô trống là \(32965\).

\(7{m^2}\,4d{m^2} = \,...\,d{m^2}\).
Số thích hợp điền vào chỗ chấm là:
A. \(74\)
B. \(704\)
C. \(740\)
D. \(7004\)
B. \(704\)
Áp dụng tính chất: \(1{m^2} = 100d{m^2}\) để đổi \(7{m^2}\) sang đơn vị \(d{m^2}\), sau đó cộng thêm với \(4d{m^2}\).
Ta có \(1{m^2} = 100d{m^2}\) nên \(7{m^2} = 700d{m^2}\).
\(7{m^2}\,4d{m^2} = 7{m^2} + 4d{m^2} = 700d{m^2} + 4d{m^2} = 704d{m^2}\)
Vậy: \(7{m^2}\,4d{m^2} \,= \,704d{m^2}\).

Điền dấu (\(>; <; =\)) thích hợp vào ô trống:
\(2002c{m^2}\,\,\)
\(\,\,20d{m^2}\,20c{m^2}\)
\(2002c{m^2}\,\,\)
\(\,\,20d{m^2}\,20c{m^2}\)
Đưa về cùng một đơn vị đo rồi so sánh kết quả với nhau.
Ta có: \(20d{m^2}\,20c{m^2} = \,20d{m^2} + 20c{m^2} = 2000c{m^2} + 20c{m^2} = 2020c{m^2}\)
Mà \(2002c{m^2} < 2020c{m^2}\)
Do đó \(2002c{m^2}\,\, < \,\,20d{m^2}\,20c{m^2}\)
Vậy đáp án đúng điền vào ô trống là \( < \).
Cho hình chữ nhật có kích thước như hình vẽ dưới đây:

Diện tích hình chữ nhật đó là:
A. \(306d{m^2}\)
B. \(316d{m^2}\)
C. \(306{m^2}\)
D. \(316{m^2}\)
A. \(306d{m^2}\)
- Đổi \(3m\,\,4dm\) sang đơn vị đo là \(dm\).
- Tính diện tích hình chữ nhật theo công thức:
Diện tích = chiều dài × chiều rộng
Đổi $3m\,\,\,4dm{\rm{ }}\; = {\rm{ }}\;34dm$
Diện tích hình chữ nhật trên là:
$34 \times 9 = 306\,\,(d{m^2})$
Đáp số: \(306d{m^2}\).

Cho hình vuông ABCD có $AB = 6m$. Hỏi diện tích hình vuông ABCD bằng bao nhiêu đề-xi-mét vuông?
A. \(36d{m^2}\)
B. \(360d{m^2}\)
C. \(3600d{m^2}\)
D. \(36000d{m^2}\)
C. \(3600d{m^2}\)
- Đổi độ dài cạnh sang đơn vị đề-xi-mét vuông rồi tính diện tích hình vuông, hoặc tính diện tích với đơn vị đo mét vuông sau đó đổi sang đơn vị đề-xi-mét vuông.
- Tính diện tích theo công thức: diện tích = cạnh × cạnh.
Đổi: \(6m = 60dm\)
Diện tích hình vuông ABCD là:
\(60 \times 60 = 3600\,\,(d{m^2})\)
Đáp số: \(3600d{m^2}\).