Trắc nghiệm Bài 34: Đoạn thẳng. Độ dài đoạn thẳng Toán 6 Kết nối tri thức
Đề bài
Kể tên các đoạn thẳng có trong hình vẽ dưới đây

-
A.
$MN;\,MQ;NQ;ML;LP;MP;NP;QL$
-
B.
$MN;QL;MQ;NQ;ML;LP;MP$
-
C.
$MN;\,MQ;NQ;ML;QL;MP;NP$
-
D.
$MN;\,MQ;ML;MP;NP$
Cho G là một điểm thuộc đoạn thẳng HK ( G không trùng với H và K). Hỏi trong ba điểm G, H, K, điểm nào nằm giữa hai điểm còn lại?
-
A.
Điểm G
-
B.
Điểm H
-
C.
Điểm K
-
D.
Không có điểm nào nằm giữa hai điểm còn lại.
Điểm \(P\) nằm giữa hai điểm \(M\) và \(N\) thì:
-
A.
$PN + MN = PN$
-
B.
$MP + MN = PN$
-
C.
$MP + PN = MN$
-
D.
$MP - PN = MN$
Nếu một đoạn thẳng cắt một tia thì đoạn thẳng và tia có bao nhiêu điểm chung?
-
A.
$1$
-
B.
$2$
-
C.
$0$
-
D.
Vô số
Cho $10$ điểm phân biệt trong đó không có ba điểm nào thẳng hàng, cứ qua hai điểm ta vẽ một đoạn thẳng. Hỏi vẽ được tất cả bao nhiêu đoạn thẳng?
-
A.
$10$
-
B.
$90$
-
C.
$40$
-
D.
$45$
Cho $n$ điểm phân biệt $\left( {n \ge 2;\,n \in N} \right)$ trong đó không có ba điểm nào thẳng hàng. Vẽ các đoạn thẳng nối hai trong $n$ điểm đó. Có tất cả $28$ đoạn thẳng. Hãy tìm $n.$
-
A.
$n = 9.$
-
B.
$n = 7.$
-
C.
$n = 8.$
-
D.
$n = 6.$
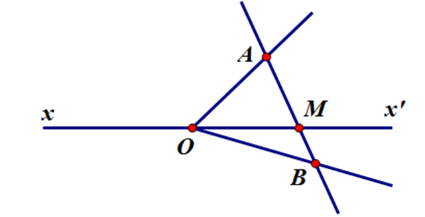
Đường thẳng \(xx'\) cắt bao nhiêu đoạn thẳng trên hình vẽ sau
-
A.
$3$
-
B.
$4$
-
C.
$5$
-
D.
$6$
Cho các đoạn thẳng \(AB = 4cm;\,MN = 5cm;\,EF = 3\,cm;\,PQ = 4cm;\,IK = 5\,cm\). Chọn đáp án sai.
-
A.
\(AB < MN\)
-
B.
$EF < IK$
-
C.
\(AB = PQ\)
-
D.
\(AB = EF\)
Hãy chọn hình vẽ đúng theo diễn đạt sau: Vẽ đoạn thẳng $AB$ không cắt đoạn thẳng $CD$ nhưng đường thẳng $AB$ cắt đoạn thẳng $CD.$
-
A.

-
B.

-
C.
-
D.
Cho $E$ là điểm nằm giữa hai điểm $I$ và $K.$ Biết rằng $IE = 4cm,EK = 10cm.$Tính độ dài đoạn thẳng $IK.$
-
A.
$4cm$
-
B.
$7cm$
-
C.
$6cm$
-
D.
$14cm$
Gọi $I$ là một điểm thuộc đoạn thẳng $MN.$ Khi $IM = 4cm,MN = 7cm$ thì độ dài của đoạn thẳng $IN$ là?
-
A.
$3cm$
-
B.
$11cm$
-
C.
$1,5cm$
-
D.
$5cm$
Gọi $K$ là một điểm của đoạn thẳng $EF.$ Biết rằng $EF = 9cm,FK = 5cm$. Khẳng định nào sau đây là đúng ?
-
A.
$EK > FK\,$
-
B.
$EK < FK$
-
C.
$EK = FK$
-
D.
$EK > EF$
Cho đoạn thẳng $AB$ có độ dài bằng $10cm.$ Điểm $M$ nằm giữa hai điểm $A$ và $B$. Biết rằng $MA = MB + 2cm.$ Tính độ dài các đoạn thẳng $MA;MB.$
-
A.
$MA = 8cm;MB = 2cm.$
-
B.
$MA = 7cm;MB = 5cm.$
-
C.
$MA = 6cm;MB = 4cm.$
-
D.
$MA = 4cm;MB = 6cm.$
Cho đoạn thẳng $IK = 8cm$. Điểm $P$ nằm giữa hai điểm $I$ và $K$ sao cho \(IP - PK = 4cm.\) Tính độ dài các đoạn thẳng $PI$ và $PK.$
-
A.
\(IP = 2cm;PK = 6cm.\)
-
B.
\(IP = 3cm;PK = 5cm.\)
-
C.
\(IP = 6cm;PK = 2cm.\)
-
D.
\(IP = 5cm;PK = 1cm.\)
Trên đường thẳng \(a\) lấy \(4\) điểm $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ theo thứ tự đó. Cho biết $MN = 2cm;MQ = 5cm$ và $NP = 1cm.$ Tìm các cặp đoạn thẳng bằng nhau.
-
A.
$MP = PQ$
-
B.
$MP = NQ$
-
C.
$MN = PQ$
-
D.
Cả B, C đều đúng.
Cho đoạn thẳng $AB = 4,5cm$ và điểm $C$ nằm giữa hai điểm $A$ và $B$. Biết $AC = \dfrac{2}{3}CB$. Tính độ dài đoạn thẳng $AC$ và $BC.$
-
A.
$BC = 2,7cm;\,AC = 1,8cm.$
-
B.
$BC = 1,8cm;\,AC = 2,7cm.$
-
C.
$BC = 1,8cm;\,AC = 1,8cm.$
-
D.
$BC = 2cm;\,AC = 3cm.$
Cho bốn điểm $A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D$ thẳng hàng theo thứ tự đó. Biết rằng \(AD = 16cm;\;AC - CD = 4cm;\;CD = 2AB.\) Tính độ dài đoạn thẳng $BD.$
-
A.
$BD = 11cm.$
-
B.
$BD = 14cm.$
-
C.
$BD = 13cm.$
-
D.
$BD = 12cm.$
Lời giải và đáp án
Kể tên các đoạn thẳng có trong hình vẽ dưới đây

-
A.
$MN;\,MQ;NQ;ML;LP;MP;NP;QL$
-
B.
$MN;QL;MQ;NQ;ML;LP;MP$
-
C.
$MN;\,MQ;NQ;ML;QL;MP;NP$
-
D.
$MN;\,MQ;ML;MP;NP$
Đáp án : A
Sử dụng định nghĩa đoạn thẳng: “Đoạn thẳng \(AB\) là hình gồm điểm A, điểm B và tất cả các điểm nằm giữa A và B” để xác định các đoạn thẳng có trên hình vẽ.
Các đoạn thẳng có trên hình vẽ là:
$MN;\,MQ;NQ;ML;LP;MP;NP;QL$
Cho G là một điểm thuộc đoạn thẳng HK ( G không trùng với H và K). Hỏi trong ba điểm G, H, K, điểm nào nằm giữa hai điểm còn lại?
-
A.
Điểm G
-
B.
Điểm H
-
C.
Điểm K
-
D.
Không có điểm nào nằm giữa hai điểm còn lại.
Đáp án : A
Dựa vào dấu hiệu nhận biết một điểm nằm giữa hai điểm.
“Nếu điểm $M$ thuộc đoạn thẳng $AB$ thì điểm $M$ nằm giữa hai điểm $A$ và $B$”
Vì G là một điểm thuộc đoạn thẳng HK nên G nằm giữa hai điểm H và K.
Điểm \(P\) nằm giữa hai điểm \(M\) và \(N\) thì:
-
A.
$PN + MN = PN$
-
B.
$MP + MN = PN$
-
C.
$MP + PN = MN$
-
D.
$MP - PN = MN$
Đáp án : C
Ta sử dụng kiến thức về cộng đoạn thẳng
Nếu điểm $M$ nằm giữa hai điểm $A$ và $B$ thì $AM + MB = AB$.

Điểm \(P\) nằm giữa hai điểm \(M\) và \(N\) thì $MP + PN = MN$.
Nếu một đoạn thẳng cắt một tia thì đoạn thẳng và tia có bao nhiêu điểm chung?
-
A.
$1$
-
B.
$2$
-
C.
$0$
-
D.
Vô số
Đáp án : A
Nếu một đoạn thẳng cắt một tia thì đoạn thẳng và tia có duy nhất một điểm chung.
Cho $10$ điểm phân biệt trong đó không có ba điểm nào thẳng hàng, cứ qua hai điểm ta vẽ một đoạn thẳng. Hỏi vẽ được tất cả bao nhiêu đoạn thẳng?
-
A.
$10$
-
B.
$90$
-
C.
$40$
-
D.
$45$
Đáp án : D
Sử dụng cách tính số đoạn thẳng:
Với \(n\) điểm cho trước \(\left( {n \in N;\,n \ge 2} \right)\) và không có ba điểm nào thẳng hàng thì số đoạn thẳng vẽ được là \(\dfrac{{n.\left( {n - 1} \right)}}{2}\) .
Số đoạn thẳng cần tìm là
$\dfrac{{10.\left( {10 - 1} \right)}}{2} = 45$ đoạn thẳng
Cho $n$ điểm phân biệt $\left( {n \ge 2;\,n \in N} \right)$ trong đó không có ba điểm nào thẳng hàng. Vẽ các đoạn thẳng nối hai trong $n$ điểm đó. Có tất cả $28$ đoạn thẳng. Hãy tìm $n.$
-
A.
$n = 9.$
-
B.
$n = 7.$
-
C.
$n = 8.$
-
D.
$n = 6.$
Đáp án : C
Sử dụng công thức tính số đoạn thẳng:
Với \(n\) điểm cho trước \(\left( {n \in N;\,n \ge 2} \right)\) và không có ba điểm nào thẳng hàng thì số đoạn thẳng vẽ được là \(\dfrac{{n.\left( {n - 1} \right)}}{2}\) .
Từ đó tìm ra $n.$
Số đoạn thẳng tạo thành từ $n$ điểm phân biệt trong đó không có ba điểm nào thẳng hàng là $\dfrac{{n\left( {n - 1} \right)}}{2}$ $\left( {n \ge 2;\,n \in N} \right)$
Theo đề bài có $28$ đoạn thẳng được tạo thành nên ta có $\dfrac{{n\left( {n - 1} \right)}}{2} = 28 \Rightarrow n\left( {n - 1} \right) = 56 = 8.7$
Nhận thấy $\left( {n - 1} \right)$ và $n$ là hai số tự nhiên liên tiếp, suy ra $n = 8.$
Đường thẳng \(xx'\) cắt bao nhiêu đoạn thẳng trên hình vẽ sau

-
A.
$3$
-
B.
$4$
-
C.
$5$
-
D.
$6$
Đáp án : C
Sử dụng kiến thức về đường thẳng và đoạn thẳng cắt nhau:
“Nếu một đoạn thẳng chỉ có một điểm chung với đường thẳng thì chúng cắt nhau.”
Đường thẳng $xx'$ cắt năm đoạn thẳng $OA;OB;AB$; $MA;MB$
Cho các đoạn thẳng \(AB = 4cm;\,MN = 5cm;\,EF = 3\,cm;\,PQ = 4cm;\,IK = 5\,cm\). Chọn đáp án sai.
-
A.
\(AB < MN\)
-
B.
$EF < IK$
-
C.
\(AB = PQ\)
-
D.
\(AB = EF\)
Đáp án : D
Sử dụng kiến thức về so sánh hai đoạn thẳng
- Hai đoạn thẳng bằng nhau nếu có cùng độ dài.
- Đoạn thẳng lớn hơn nếu có độ dài lớn hơn.
+ Đáp án A: \(AB < MN\) là đúng vì $AB = 4cm < 5cm = MN$.
+ Đáp án B: $EF < IK$ là đúng vì $EF = 3cm < 5cm = IK$
+ Đáp án C: \(AB = PQ\) là đúng vì hai đoạn cùng có độ dài $4cm$
+ Đáp án D: \(AB = EF\) là sai vì $AB = 4cm > 3cm = EF$.
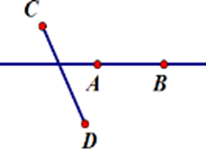
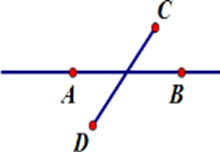
Hãy chọn hình vẽ đúng theo diễn đạt sau: Vẽ đoạn thẳng $AB$ không cắt đoạn thẳng $CD$ nhưng đường thẳng $AB$ cắt đoạn thẳng $CD.$
-
A.

-
B.

-
C.

-
D.

Đáp án : C
Sử dụng kiến thức:
Nếu một đoạn thẳng chỉ có một điểm chung với đường thẳng, tia hoặc đoạn thẳng khác thì chúng cắt nhau.
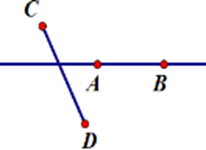
Đoạn thẳng $AB$ không cắt đoạn thẳng $CD$ nhưng đường thẳng $AB$ cắt đoạn thẳng $CD$ nghĩa là đoạn thẳng $AB$ không có điểm chung với đoạn thẳng $CD$ và đường thẳng $AB$có duy nhất một điểm chung với đoạn thẳng $CD.$
Hình vẽ thể hiện đúng diễn đạt trên là
Cho $E$ là điểm nằm giữa hai điểm $I$ và $K.$ Biết rằng $IE = 4cm,EK = 10cm.$Tính độ dài đoạn thẳng $IK.$
-
A.
$4cm$
-
B.
$7cm$
-
C.
$6cm$
-
D.
$14cm$
Đáp án : D
$E$ là điểm nằm giữa hai điểm $I$ và $K$ nên ta có công thức cộng đoạn thẳng $IE + EK = IK$. Biết độ dài $IL, LK$, thay số vào ta tính được độ dài đoạn thẳng $IK.$
Vì $E$ là điểm nằm giữa hai điểm $I$ và $K$ nên ta có $IE + EK = IK$
Hay $4 + 10 = IK$ suy ra $IK = 14\,cm.$
Gọi $I$ là một điểm thuộc đoạn thẳng $MN.$ Khi $IM = 4cm,MN = 7cm$ thì độ dài của đoạn thẳng $IN$ là?
-
A.
$3cm$
-
B.
$11cm$
-
C.
$1,5cm$
-
D.
$5cm$
Đáp án : A
+ Chỉ ra rằng $I$ nằm giữa hai điểm $M;N$ dựa vào kiến thức: “Nếu điểm $M$ thuộc đoạn thẳng $AB$ thì điểm $M$ nằm giữa hai điểm $A$ và $B$”
+ Sử dụng công thức cộng đoạn thẳng: $MI + IN = MN$ để suy ra độ dài đoạn thẳng chưa biết.
Vì $I$ là một điểm thuộc đoạn thẳng $MN$ nên $I$ là điểm nằm giữa hai điểm $M;N$.
Do đó ta có $MI + IN = MN$ mà $IM = 4cm,MN = 7cm$ nên $4 + IN = 7 \Rightarrow IN = 7 - 4$$ \Rightarrow IN = 3\,cm.$
Gọi $K$ là một điểm của đoạn thẳng $EF.$ Biết rằng $EF = 9cm,FK = 5cm$. Khẳng định nào sau đây là đúng ?
-
A.
$EK > FK\,$
-
B.
$EK < FK$
-
C.
$EK = FK$
-
D.
$EK > EF$
Đáp án : B
Dựa vào dấu hiệu nhận biết điểm nằm giữa hai điểm để chỉ ra $K$ nằm giữa $E;F$.
Từ đó sử dụng công thức cộng đoạn thẳng để tính độ dài đoạn thẳng $EK$.
Thực hiện phép so sánh các đoạn thẳng để chọn đáp án đúng.
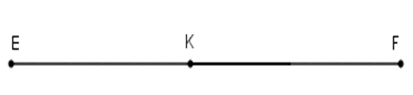
Vì $K$ là một điểm của đoạn thẳng $EF$ nên điểm $K$ nằm giữa $E;F$. Do đó ta có
$EK + KF = EF \Rightarrow EK = EF - KF$$ \Rightarrow EK = 9 - 5 = 4cm$.
Suy ra $EK < FK\,\left( {4cm < 5cm} \right)$ nên A và C sai, B đúng.
Vì $4cm < 7cm$ nên $EK < EF$ do đó D sai.
Cho đoạn thẳng $AB$ có độ dài bằng $10cm.$ Điểm $M$ nằm giữa hai điểm $A$ và $B$. Biết rằng $MA = MB + 2cm.$ Tính độ dài các đoạn thẳng $MA;MB.$
-
A.
$MA = 8cm;MB = 2cm.$
-
B.
$MA = 7cm;MB = 5cm.$
-
C.
$MA = 6cm;MB = 4cm.$
-
D.
$MA = 4cm;MB = 6cm.$
Đáp án : C
Sử dụng công thức cộng đoạn thẳng $AM + MB = AB$ và dữ kiện đề bài để tìm độ dài hai đoạn thẳng $MA;MB.$

Vì điểm $M$ nằm giữa hai điểm $A$ và $B$ nên ta có $MA + MB = AB$ (1)
Thay $MA = MB + 2$ vào (1) ta được $MB + 2 + MB = AB$ mà $AB = 10cm$
Suy ra $2MB + 2 = 10 \Rightarrow 2MB = 10 - 2 \Rightarrow 2MB = 8$$ \Rightarrow MB = 8:2 = 4cm$
Nên $MA = MB + 2 = 4 + 2 = 6cm$.
Vậy $MA = 6cm;MB = 4cm.$
Cho đoạn thẳng $IK = 8cm$. Điểm $P$ nằm giữa hai điểm $I$ và $K$ sao cho \(IP - PK = 4cm.\) Tính độ dài các đoạn thẳng $PI$ và $PK.$
-
A.
\(IP = 2cm;PK = 6cm.\)
-
B.
\(IP = 3cm;PK = 5cm.\)
-
C.
\(IP = 6cm;PK = 2cm.\)
-
D.
\(IP = 5cm;PK = 1cm.\)
Đáp án : C
Sử dụng công thức cộng đoạn thẳng $PI + IK = PK$ và dữ kiện đề bài để tìm độ dài hai đoạn thẳng $PI;PK.$

Vì điểm $P$ nằm giữa hai điểm $I$ và $K$ nên ta có $PI + PK = IK \Rightarrow PI + IK = 8cm$ (1)
Theo đề bài \(IP - PK = 4cm\)(2)
Từ (1) và (2) suy ra \(IP = \dfrac{{8 + 4}}{2} = 6cm\) và \(PK = \dfrac{{8 - 4}}{2} = 2cm\)
Vậy \(IP = 6cm;PK = 2cm.\)
Trên đường thẳng \(a\) lấy \(4\) điểm $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ theo thứ tự đó. Cho biết $MN = 2cm;MQ = 5cm$ và $NP = 1cm.$ Tìm các cặp đoạn thẳng bằng nhau.
-
A.
$MP = PQ$
-
B.
$MP = NQ$
-
C.
$MN = PQ$
-
D.
Cả B, C đều đúng.
Đáp án : D
Chỉ ra các điểm nằm giữa hai điểm còn lại, sau đó sử dụng công thức cộng đoạn thẳng để tính độ dài các đoạn thẳng.
Tìm ra các đoạn thẳng có độ dài bằng nhau.
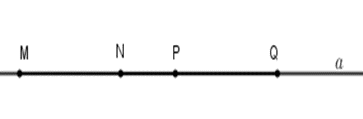
Theo đề bài ta có $N$ nằm giữa $M$ và $Q$ nên $MN + NQ = MQ$ mà $MN = 2cm;MQ = 5cm$
Nên $NQ = MQ - MN = 5 - 2 = 3cm$.
Lại có $P$ nằm giữa $N$ và $Q$ (theo đề bài) nên $NP + PQ = NQ$ mà $NP = 1cm;\,NQ = 3cm$
Nên $PQ = NQ - NP = 3 - 1 = 2cm$
Vì $N$ nằm giữa $M$ và $P$ (theo đề bài) nên $MN + NP = MP$ mà $NP = 1cm;\,MN = 2cm$
Nên $MP = 2 + 1 = 3cm$
Khi đó ta có $NQ = 3cm;MP = 3cm;PQ = 2cm;MN = 2cm$ nên $NQ = MP;\,MN = PQ$; $MP < PQ$.
Vậy A sai và cả B, C đều đúng.
Cho đoạn thẳng $AB = 4,5cm$ và điểm $C$ nằm giữa hai điểm $A$ và $B$. Biết $AC = \dfrac{2}{3}CB$. Tính độ dài đoạn thẳng $AC$ và $BC.$
-
A.
$BC = 2,7cm;\,AC = 1,8cm.$
-
B.
$BC = 1,8cm;\,AC = 2,7cm.$
-
C.
$BC = 1,8cm;\,AC = 1,8cm.$
-
D.
$BC = 2cm;\,AC = 3cm.$
Đáp án : A
Sử dụng công thức cộng đoạn thẳng $AC + CB = AB$ và dữ kiện đề bài $AC = \dfrac{2}{3}CB$ để tính độ dài mỗi đoạn thẳng $AC$ và $BC.$
Vì điểm $C$ nằm giữa hai điểm $A$ và $B$ nên ta có $AC + CB = AB$ (1)
Thay $AC = \dfrac{2}{3}CB$ (theo đề bài) vào (1) ta được $\dfrac{2}{3}CB + CB = AB$ $ \Rightarrow CB.\left( {\dfrac{2}{3} + 1} \right) = 4,5$
$ \Rightarrow CB.\dfrac{5}{3} = \dfrac{9}{2}$$ \Rightarrow BC = \dfrac{9}{2}:\dfrac{5}{3} = \dfrac{{27}}{{10}} = 2,7\,cm$
Từ đó $AC = \dfrac{2}{3}BC = \dfrac{2}{3}.2,7 = 1,8cm$.
Vậy $BC = 2,7cm;\,AC = 1,8cm.$
Cho bốn điểm $A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D$ thẳng hàng theo thứ tự đó. Biết rằng \(AD = 16cm;\;AC - CD = 4cm;\;CD = 2AB.\) Tính độ dài đoạn thẳng $BD.$
-
A.
$BD = 11cm.$
-
B.
$BD = 14cm.$
-
C.
$BD = 13cm.$
-
D.
$BD = 12cm.$
Đáp án : C
Từ đề bài suy ra các điểm nằm giữa hai điểm còn lại. Sử dụng công thức cộng đoạn thẳng và các dữ kiện đề bài để tính toán.

Theo đề bài điểm $C$ nằm giữa hai điểm $A$ và $D$ nên ta có $AC + CD = AD$
Mà $AD = 16cm$ nên $AC + CD = 16cm$ và $AC - CD = 4cm$
Suy ra $AC = \dfrac{{16 + 4}}{2} = 10cm$ và $CD = \dfrac{{16 - 4}}{2} = 6cm$.
Lại có $CD = 2AB$ nên $AB = \dfrac{{CD}}{2} = \dfrac{6}{2} = 3cm$.
Theo đề bài ta có điểm $B$ nằm giữa hai điểm $A$ và $D$ nên $AB + BD = AD$
Suy ra $3 + BD = 16 \Rightarrow BD = 16 - 3 = 13\,cm.$
Vậy $BD = 13cm.$