Trắc nghiệm toán 6 bài 7 chương 5 chân trời sáng tạo có đáp án — Không quảng cáo

+ Nếu phân số dương lớn hơn $1,$  ta có thể viết nó dưới dạng hỗn số bằng cách: chia tử cho mẫu, thương tìm được là phần nguyên của hỗn số, số dư là tử của phân số kèm theo, còn mẫu vẫn là mẫu đã cho.

Ta có: $4:3$ bằng $1$ (dư $1$ ) nên $\dfrac{4}{3} = 1\dfrac{1}{3}$

Quy tắc đổi hỗn số:

Đối với các hỗn số có dấu $'' - ''$ đằng trước thì ta chỉ cần đổi phần hỗn số dương theo quy tắc thông thường rồi viết thêm dấu $'' - ''$ đằng trước phân số tìm được, tuyệt đối không lấy phần số nguyên âm nhân với mẫu rồi cộng tử số.

$- 2\dfrac{3}{4} =  - \dfrac{{2.4 + 3}}{4} =  - \dfrac{{11}}{4}$

Sử dụng quy tắc đổi hỗn số ra phân số:

Muốn viết một hỗn số dưới dạng một phân số, ta nhân phần nguyên với mẫu rồi cộng với tử, kết quả tìm được là tử của phân số, còn mẫu vẫn là mẫu đã cho.

Đáp án A:

$\dfrac{1}{{19}} + \dfrac{1}{{20}} = \dfrac{{20}}{{19.20}} + \dfrac{{19}}{{19.20}}$ $= \dfrac{{19 + 20}}{{19.20}} \ne \dfrac{{19.20}}{{19 + 20}}$

Nên A sai.

Đáp án B: $6\dfrac{{23}}{{11}} = \dfrac{{6.11 + 23}}{{11}} \ne \dfrac{{6.23 + 11}}{{11}}$ nên B sai.

Đáp án C: $a\dfrac{a}{{99}} = \dfrac{{a.99 + a}}{{99}}$$= \dfrac{{a.\left( {99 + 1} \right)}}{{99}} = \dfrac{{100a}}{{99}}$ nên C đúng.

Đáp án D: $1\dfrac{{15}}{{23}} = \dfrac{{1.23 + 15}}{{15}} \ne \dfrac{{1.23}}{{15}}$ nên D sai.

Hỗn số gồm:

Phần nguyên = số giờ

Phần phân số = Số phút: 60

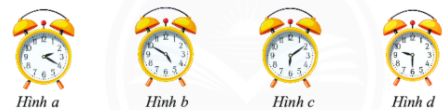
Hình a: $2\dfrac{1}{3}$

Hình b: $4\dfrac{5}{6}$

Hình c: $6\dfrac{1}{6}$

Hình d: $9\dfrac{1}{2}$

Vậy ta được các hỗn số: $2\dfrac{1}{3}$; $4\dfrac{5}{6}$; $6\dfrac{1}{6}$; $9\dfrac{1}{2}$.

Đổi các khối lượng ra các phân số có cùng đơn vị đo khối lượng, sau đó sắp xếp các phân số đó theo thứ tự từ lớn đến nhỏ.

Ta có:

$3\dfrac{3}{4}$ tạ = $\dfrac{{15}}{4}$ tạ = $\dfrac{{375}}{{100}}$ tạ.

$\dfrac{7}{2}$ tạ = $\dfrac{{350}}{{100}}$ tạ

$3\dfrac{{45}}{{100}}$ tạ = $\dfrac{{345}}{{100}}$ tạ

$365$kg = $\dfrac{{365}}{{100}}$ tạ

=> Các khối lượng theo thứ tự từ lớn đến nhỏ là:

$\dfrac{{377}}{{100}}$ tạ ; $3\dfrac{3}{4}$ tạ; $365$kg; $\dfrac{7}{2}$ tạ; $3\dfrac{{45}}{{100}}$ tạ.

Đổi các khối lượng ra các phân số có cùng đơn vị đo khối lượng

a) $125\,d{m^2} = \dfrac{{125}}{{100}}{m^2} = 1\dfrac{{25}}{{100}}\,{m^2}$

b) $218\,c{m^2} = \dfrac{{218}}{{10000}}{m^2} = \dfrac{{109}}{{5000}}\,{m^2}$

c) $240\,d{m^2} = \dfrac{{240}}{{100}}{m^2} = 2\dfrac{{40}}{{100}}\,{m^2}$

d) $34\,c{m^2} = \dfrac{{34}}{{10000}}{m^2} = \dfrac{{17}}{{5000}}\,{m^2}$

Vậy ta được: $1\dfrac{{25}}{{100}}\,{m^2}$; $\dfrac{{109}}{{5000}}\,{m^2}$; $2\dfrac{{40}}{{100}}\,{m^2}$; $\dfrac{{17}}{{5000}}\,{m^2}$.

Đổi thời gian ra giờ.

Tính vận mỗi xe = Quãng đường : thời gian mỗi xe đi

=> So sánh hỗn số => So sánh được vận tốc hai xe.

Đổi 70 phút = $\dfrac{7}{6}$ giờ

Vận tốc của xe taxi là:

100 : $1\dfrac{1}{5}$ = 100 : $\dfrac{6}{5}$ = $\dfrac{{250}}{3}$ = $83\dfrac{1}{3}$ (km/h)

Vận tốc của xe tải là:

100 : $\dfrac{7}{6}$ = $\dfrac{{600}}{7}$ = $85\dfrac{5}{7}$ (km/h)

Ta có: $85\dfrac{5}{7}$ > $83\dfrac{1}{3}$ nên vận tốc của xe tải lớn hơn vận tốc xe taxi.

a giờ b phút = $a + \dfrac{b}{{60}}$ (giờ)

2 giờ 15 phút = $2 + \dfrac{{15}}{{60}} = 2 + \dfrac{1}{4} = 2\dfrac{1}{4}$ giờ.

Đổi hỗn số ra phân số rồi thực hiện phép cộng hai phân số.

$\left( { - 2\dfrac{1}{4}} \right) + \dfrac{5}{2} =  - \dfrac{9}{4} + \dfrac{5}{2}$$= \dfrac{{ - 9}}{4} + \dfrac{{10}}{4} = \dfrac{1}{4}$

Đổi hỗn số thành phân số, đồng thời rút gọn phân số có thể rút gọn được, từ đó tìm $x$

$\begin{array}{l}2\dfrac{x}{7} = \dfrac{{75}}{{35}}\\\dfrac{{2.7 + x}}{7} = \dfrac{{15}}{7}\\14 + x = 15\\x = 15 - 14\\x = 1\end{array}$

Đổi hỗn số thành phân số rồi cộng các phân số với nhau.

$\left( { - 1\dfrac{1}{3}} \right) + 2\dfrac{1}{2} =  - \dfrac{4}{3} + \dfrac{5}{2}$$= \dfrac{{ - 8}}{6} + \dfrac{{15}}{6} = \dfrac{7}{6}$

Đổi hỗn số ra phân số, đặt $x$ làm thừa số chung rồi tìm $x$ theo phương pháp tìm thừa số chưa biết trong một tích.

$\begin{array}{l}x - 3\dfrac{1}{2}x =  - \dfrac{{20}}{7}\\x - \dfrac{7}{2}x =  - \dfrac{{20}}{7}\\x.\left( {1 - \dfrac{7}{2}} \right) =  - \dfrac{{20}}{7}\\x.\left( {\dfrac{{ - 5}}{2}} \right) = \dfrac{{ - 20}}{7}\\x = \dfrac{{ - 20}}{7}:\dfrac{{ - 5}}{2}\\x = \dfrac{{ - 20}}{7}.\dfrac{2}{{ - 5}}\\x = \dfrac{8}{7} \\x= 1\dfrac{1}{7}\end{array}$

- Thực hiện các phép tính ở mỗi đáp án.

- Kết luận.

Chú ý: Đổi các hỗn số thành phân số rồi thực hiện cộng, trừ, nhân, chia các phân số.

Đáp án A: $\left( { - 3\dfrac{3}{4}} \right).1\dfrac{1}{2}$$=  - \dfrac{{15}}{4}.\dfrac{3}{2} =  - \dfrac{{45}}{8} =  - 5\dfrac{5}{8} \ne  - 3\dfrac{3}{8}$

Nên A sai.

Đáp án B: $3\dfrac{3}{4}:1\dfrac{1}{5} = \dfrac{{15}}{4}:\dfrac{6}{5} = \dfrac{{15}}{4}.\dfrac{5}{6}$$= \dfrac{{25}}{8} = 3\dfrac{1}{8} \ne 3\dfrac{3}{{20}}$ nên B sai.

Đáp án C: $\left( { - 3} \right) - \left( { - 2\dfrac{2}{5}} \right)$$= \left( { - 3} \right) - \left( { - \dfrac{{12}}{5}} \right) = \left( { - 3} \right) + \dfrac{{12}}{5} = \dfrac{{ - 3}}{5}$

Nên C đúng.

Đáp án D: $5\dfrac{7}{{10}}.15 = \dfrac{{57}}{{10}}.15 = \dfrac{{171}}{2} \ne \dfrac{{105}}{2}$ nên D sai.

Phá ngoặc rồi nhóm các hỗn số có tổng hoặc hiệu là một số nguyên để tính toán cho nhanh.

$A = \left( {4\dfrac{5}{{17}} - 3\dfrac{4}{5} + 8\dfrac{{15}}{{29}}} \right) - \left( {3\dfrac{5}{{17}} - 6\dfrac{{14}}{{29}}} \right)$

$A = 4\dfrac{5}{{17}} - 3\dfrac{4}{5} + 8\dfrac{{15}}{{29}} - 3\dfrac{5}{{17}} + 6\dfrac{{14}}{{29}}$

$A = \left( {4\dfrac{5}{{17}} - 3\dfrac{5}{{17}}} \right) + \left( {8\dfrac{{15}}{{29}} + 6\dfrac{{14}}{{29}}} \right) - 3\dfrac{4}{5}$

$A = \left( {4 - 3} \right) + \left( {\dfrac{5}{{17}} - \dfrac{5}{{17}}} \right)$ $+ \left( {8 + 6} \right) + \left( {\dfrac{{15}}{{29}} + \dfrac{{14}}{{29}}} \right) - 3\dfrac{4}{5}$

$A = 1 + 0 + 14 + 1 - 3\dfrac{4}{5}$

$A=16-3\dfrac{4}{5}$

$A = 15\dfrac{5}{5} - 3\dfrac{4}{5} = 12\dfrac{1}{5}$

Thu gọn $M$ rồi thay $x =  - 8\dfrac{7}{{10}}$ vào tính giá trị của $M$

$M = 60\dfrac{7}{{13}}.x + 50\dfrac{8}{{13}}.x - 11\dfrac{2}{{13}}.x$

$M = \left( {60\dfrac{7}{{13}} + 50\dfrac{8}{{13}} - 11\dfrac{2}{{13}}} \right).x$

$M = \left[ {\left( {60 + 50 - 11} \right) + \left( {\dfrac{7}{{13}} + \dfrac{8}{{13}} - \dfrac{2}{{13}}} \right)} \right].x$

$M = \left( {99 + 1} \right).x = 100x$

Thay $x =  - 8\dfrac{7}{{10}}$ vào $M$ ta được:

$M = 100.\left( { - 8\dfrac{7}{{10}}} \right)$ $= 100.\left( { - \dfrac{{87}}{{10}}} \right) =  - 870$

Rút gọn vế trái và vế phải bằng cách đưa hỗn số về phân số. Từ đó chọn số phù hợp.

$\begin{array}{l}6\dfrac{1}{3}:4\dfrac{2}{9} < x < \left( {10\dfrac{2}{9} + 2\dfrac{2}{5}} \right) - 6\dfrac{2}{9}\\\dfrac{{19}}{3}:\dfrac{{38}}{9} < x < \dfrac{{92}}{9} + \dfrac{{12}}{5} - \dfrac{{56}}{9}\\\dfrac{3}{2} < x < \dfrac{{32}}{5}\end{array}$

Ta có:

$\begin{array}{l}\dfrac{3}{2} < x < \dfrac{{32}}{5}\\1,5 < x < 6,4\end{array}$

Vì x là số tự nhiên nên $x \in \left\{ {2;3;4;5;6} \right\}$.