Trắc nghiệm Bài 6: Chia hết và chia có dư. Tính chất chia hết của một tổng Toán 6 Chân trời sáng tạo
Đề bài
Nếu $a$ không chia hết cho $2$ và $b$ chia hết cho $2$ thì tổng \(a + b\)
-
A.
chia hết cho $2$
-
B.
không chia hết cho $2$
-
C.
có tận cùng là $2$
-
D.
có tận cùng là $1;3;7;9$
Tổng nào sau đây chia hết cho $7$
-
A.
\(49 + 70\)
-
B.
\(14 + 51\)
-
C.
\(7 + 134\)
-
D.
\(10 + 16\)
Khẳng định nào sau đây đúng ?
-
A.
\(250 \vdots 25\)
-
B.
\(51 \vdots 7\)
-
C.
\(36 \vdots 16\)
-
D.
\(48 \vdots 18\)
1560:15 bằng
-
A.
14
-
B.
104
-
C.
41
-
D.
401
Khẳng định nào sau đây sai ?
-
A.
\(199\not \vdots 2\)
-
B.
\(199\not \vdots 3\)
-
C.
\(199\not \vdots 7\)
-
D.
\(199 \vdots 11\)
Cho \(a \vdots m\) và \(b \vdots m\) và \(c \vdots m\) với m là số tự nhiên khác 0. Các số a,b,c là số tự nhiên tùy ý.
Khẳng định nào sau đây chưa đúng?
(Xét trong tập số tự nhiên, số bị trừ phải lớn hơn hoặc bằng số trừ)
-
A.
\(\left( {a + b} \right) \vdots m\)
-
B.
\(\left( {a - b} \right) \vdots m\)
-
C.
\(\left( {a + b + c} \right) \vdots m\)
-
D.
\(\left( {b + c} \right) \vdots m\)
Nếu \(x \, \vdots \, 2\) và \(y \, \vdots \, 4\) thì tổng \(x + y\) chia hết cho
-
A.
$2$
-
B.
$4$
-
C.
$8$
-
D.
không xác định
Nếu \(x \, \vdots \, 12\) và \(y \, \vdots \, 8\) thì hiệu \(x - y\) chia hết cho
-
A.
$6$
-
B.
$3$
-
C.
$4$
-
D.
$12$
Chọn câu sai.
-
A.
\(49 + 105 + 399\) chia hết cho \(7\) .
-
B.
\(84 + 48 + 120\) không chia hết cho \(8\)
-
C.
$18 + 54 + 12$ chia hết cho \(9\)
-
D.
$18 + 54 + 12$ không chia hết cho \(9\)
Cho tổng \(M = 75 + 120 + x\) . Với giá trị nào của \(x\) dưới đây thì \(M \, \vdots \, 3?\)
-
A.
$7$
-
B.
$5$
-
C.
$4$
-
D.
$12$
Lời giải và đáp án
Nếu $a$ không chia hết cho $2$ và $b$ chia hết cho $2$ thì tổng \(a + b\)
-
A.
chia hết cho $2$
-
B.
không chia hết cho $2$
-
C.
có tận cùng là $2$
-
D.
có tận cùng là $1;3;7;9$
Đáp án : B
Tính chất 2: Nếu chỉ có một số hạng của tổng không chia hết cho một số còn các số hạng khác đều chia hết cho số đó thì tổng không chia hết cho số đó.
Theo tính chất 2: nếu $a$ không chia hết cho $2$và $b$ chia hết cho $2$ thì \(a + b\) không chia hết cho $2.$
Tổng nào sau đây chia hết cho $7$
-
A.
\(49 + 70\)
-
B.
\(14 + 51\)
-
C.
\(7 + 134\)
-
D.
\(10 + 16\)
Đáp án : A
Tính chất 1: Nếu số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
Ta có: \(49 \vdots 7;\,\,\,70 \vdots 7 \Rightarrow \left( {49 + 70} \right) \vdots 7\) (theo tính chất 1)
Khẳng định nào sau đây đúng ?
-
A.
\(250 \vdots 25\)
-
B.
\(51 \vdots 7\)
-
C.
\(36 \vdots 16\)
-
D.
\(48 \vdots 18\)
Đáp án : A
Cho hai số tự nhiên \(a\) và \(b,\) trong đó \(b \ne 0,\) nếu có số tự nhiên \(x\) sao cho \(b.x = a\) thì ta nói \(a\) chia hết cho \(b\) và ta có phép chia hết \(a:b = x\) , kí hiệu là \(a \vdots b\) .
Ta có: 25.10=250 nên \(250 \vdots 25\)
1560:15 bằng
-
A.
14
-
B.
104
-
C.
41
-
D.
401
Đáp án : B
Đặt tính rồi tính.
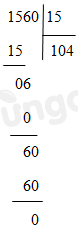
Vậy \(1560 = 15.104\) . Hay thương của phép chia 1560 cho 15 là 104.
Khẳng định nào sau đây sai ?
-
A.
\(199\not \vdots 2\)
-
B.
\(199\not \vdots 3\)
-
C.
\(199\not \vdots 7\)
-
D.
\(199 \vdots 11\)
Đáp án : D
Đặt tính rồi tính.
199 đều không chia hết cho 2, 3, 7 và 11 nên \(199\not \vdots 11\)
Cho \(a \vdots m\) và \(b \vdots m\) và \(c \vdots m\) với m là số tự nhiên khác 0. Các số a,b,c là số tự nhiên tùy ý.
Khẳng định nào sau đây chưa đúng?
(Xét trong tập số tự nhiên, số bị trừ phải lớn hơn hoặc bằng số trừ)
-
A.
\(\left( {a + b} \right) \vdots m\)
-
B.
\(\left( {a - b} \right) \vdots m\)
-
C.
\(\left( {a + b + c} \right) \vdots m\)
-
D.
\(\left( {b + c} \right) \vdots m\)
Đáp án : B
Tính chất 1 : Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
\(a \vdots m\) và \(b \vdots m\) \( \Rightarrow \left( {a + b} \right) \vdots m\)
\(a \vdots m\) và \(b \vdots m\) \( \Rightarrow \left( {a - b} \right) \vdots m\) với \(\left( {a \ge b} \right)\)
\(a \vdots m;b \vdots m;c \vdots m \Rightarrow \left( {a + b + c} \right) \vdots m\)
\(\left( {a - b} \right) \vdots m\) sai vì thiếu điều kiện \(a \ge b\)
Nếu \(x \, \vdots \, 2\) và \(y \, \vdots \, 4\) thì tổng \(x + y\) chia hết cho
-
A.
$2$
-
B.
$4$
-
C.
$8$
-
D.
không xác định
Đáp án : A
Tính chất 1: Nếu số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
Ta có: \(x\,\, \vdots \,\,2;\,\,y\,\, \vdots \,\,4 \Rightarrow y\,\, \vdots \,\,2 \Rightarrow \left( {x + y} \right)\,\, \vdots \,\,2\)
Nếu \(x \, \vdots \, 12\) và \(y \, \vdots \, 8\) thì hiệu \(x - y\) chia hết cho
-
A.
$6$
-
B.
$3$
-
C.
$4$
-
D.
$12$
Đáp án : C
Nếu số hạng của một hiệu đều chia hết cho cùng một số thì hiệu chia hết cho số đó.
Ta có: \(\left\{ \begin{array}{l}x \, \vdots \, 12 \Rightarrow x \, \vdots \, 4\\y \, \vdots \, 8 \Rightarrow y \, \vdots \, 4\end{array} \right.\) .
Vì \(x \, \vdots \, 4;y \, \vdots \, 4 \Rightarrow \left( {x - y} \right) \, \vdots \, 4\) .
Chọn câu sai.
-
A.
\(49 + 105 + 399\) chia hết cho \(7\) .
-
B.
\(84 + 48 + 120\) không chia hết cho \(8\)
-
C.
$18 + 54 + 12$ chia hết cho \(9\)
-
D.
$18 + 54 + 12$ không chia hết cho \(9\)
Đáp án : C
+ TC1: Nếu số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
+ TC2: Nếu chỉ có một số hạng của tổng không chia hết cho một số còn các số hạng khác đều chia hết cho số đó thì tổng không chia hết cho số đó.
+) Vì \(49\,\, \vdots \,\,7;\,\,105\,\, \vdots \,\,7;\,\,399\,\, \vdots \,\,7 \Rightarrow \left( {49 + 105 + 399} \right)\,\, \vdots \,\,7\) ( theo tính chất 1) nên A đúng
+) Vì \(48\,\, \vdots \,\,8;\,\,120\,\, \vdots\,\, 8\) mà 84 không chia hết cho 8 nên \(84 + 48 + 120\) không chia hết cho 8 nên B đúng
+) Vì \(18\,\, \vdots\,\, 9;\,\,54\,\, \vdots\,\, 9\) mà 12 không chia hết cho 9 nên \(18 + 54 + 12\) không chia hết cho 9 nên C sai, D đúng.
Cho tổng \(M = 75 + 120 + x\) . Với giá trị nào của \(x\) dưới đây thì \(M \, \vdots \, 3?\)
-
A.
$7$
-
B.
$5$
-
C.
$4$
-
D.
$12$
Đáp án : D
Sử dụng tính chất 1: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó. \(a\, \vdots \,m;\,b\, \vdots \,m;\,c\, \vdots \,m \Rightarrow \left( {a + b + c} \right) \vdots \,m\)
Vì \(75\, \vdots \,3;\,120\, \vdots \,3\) nên để \(M = 75 + 120 + x\) chia hết cho \(3\) thì \(x\, \vdots \,3\) nên ta chọn \(x = 12.\)