Trắc nghiệm Bài 4: Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh Toán 7 Cánh diều
Đề bài
Trên đường thẳng \(xy\) lấy hai điểm \(A,B\). Trên cùng nửa mặt phẳng bờ \(xy\) lấy hai điểm \(C\) và \(C'\) sao cho \(AC = BC';BC = AC'.\)
Chọn câu đúng.
-
A.
\(\widehat {BCA} = \widehat {BAC'}\)
-
B.
\(\Delta ACB = \Delta BAC'\)
-
C.
\(\widehat {BCA} = \widehat {ABC'}\)
-
D.
\(\Delta ACB = \Delta BC'A\)
So sánh hai góc \(\widehat {CAC'};\,\widehat {CBC'}\)?
-
A.
\(\widehat {CAC'} > \widehat {CBC'}\)
-
B.
\(\widehat {CAC'} < \widehat {CBC'}\)
-
C.
\(\widehat {CAC'} = \widehat {CBC'}\)
-
D.
\(\widehat {CAC'} = 2.\widehat {CBC'}\)
Cho \(\widehat {xOy} = {50^0}\), vẽ cung tròn tâm $O$ bán kính bằng $2cm,$ cung tròn này cắt $Ox, Oy$ lần lượt ở $A$ và $B.$ Vẽ các cung tròn tâm $A$ và tâm $B$ có bán kính $3cm,$ chúng cắt nhau tại điểm $C$ nằm trong góc $xOy.$ Tính \(\widehat {xOC}\) .
-
A.
\({25^0}\)
-
B.
\({50^0}\)
-
C.
\({80^0}\)
-
D.
\({90^0}\)
Cho tam giác $ABC$ có $AB < AC$ . Gọi \(E \in AC\) sao cho \(AB = CE\). Gọi $O$ là một điểm nằm ở trong tam giác sao cho $OA = OC,OB = OE.$ Khi đó:
-
A.
\(\Delta AOB = \Delta CEO\)
-
B.
\(\Delta AOB = \Delta COE\)
-
C.
\(\widehat {AOB} = \widehat {OEC}\)
-
D.
\(\widehat {ABO} = \widehat {OCE}\)
Cho tam giác $MNP$ có $MN = MP.$ Gọi $A$ là trung điểm của $NP.$ Biết \(\widehat {NMP} = {40^0}\) thì số đo góc $MPN$ là:
-
A.
\({100^0}\)
-
B.
\({70^0}\)
-
C.
\({80^0}\)
-
D.
\({90^0}\)
Cho tam giác $ABC$ có $AB = AC$ và $MB = MC$ (\(M \in BC\)). Chọn câu sai.
-
A.
$\Delta AMC = \Delta BCM$
-
B.
$AM \bot BC$
-
C.
\(\widehat {BAM} = \widehat {CAM}\)
-
D.
\(\Delta AMB = \Delta AMC\)
Cho đoạn thẳng \(AB = 6cm.\) Trên một nửa mặt hẳng bờ $AB$ vẽ tam giác $ABC$ sao cho \(AC = 4cm,\) \(BC = 5cm,\) trên nửa mặt phẳng còn lại vẽ tam giác $ABD$ sao cho \(BD = 4cm,\) \(AD = 5cm.\) Chọn câu đúng.
-
A.
\(\Delta CAB = \Delta DAB\)
-
B.
\(\Delta ABC = \Delta BDA\)
-
C.
\(\Delta CAB = \Delta DBA\)
-
D.
\({\rm{\Delta CAB = \Delta {\rm A}{\rm B}D}}\)
Cho tam giác $ABD$ và tam giác $IKH$ có $AB = KI,AD = KH,DB = IH.$
Phát biểu nào trong các phát biểu sau đây là đúng :
-
A.
\(\Delta BAD = \Delta HIK\)
-
B.
\(\Delta ABD = \Delta KHI\)
-
C.
\(\Delta DAB = \Delta HIK\)
-
D.
\(\Delta ABD = \Delta KIH\)
Nếu \(\widehat A = {60^ \circ }\), thì số đo góc $K$ là:
-
A.
\({60^ \circ }\)
-
B.
\({70^ \circ }\)
-
C.
\({90^ \circ }\)
-
D.
\({120^ \circ }\)
Cho hình dưới đây.
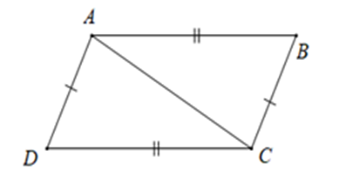
Chọn câu sai .
-
A.
\(AD//BC\)
-
B.
\(AB//CD\)
-
C.
\(\Delta ABC = \Delta CDA\)
-
D.
\(\Delta ABC = \Delta ADC\)
Cho hai tam giác $ABD$ và $CDB$ có cạnh chung $BD.$ Biết $AB = DC$ và $AD = CB.$ Phát biểu nào sau đây là sai :
-
A.
\(\Delta ABC = \Delta CDA\)
-
B.
\(\widehat {ABC} = \widehat {CDA}\)
-
C.
\(\widehat {BAC} = \widehat {DAC}\)
-
D.
\(\widehat {BCA} = \widehat {DAC}\)
Cho hình vẽ sau. Tam giác nào bằng với tam giác \(ABC?\)
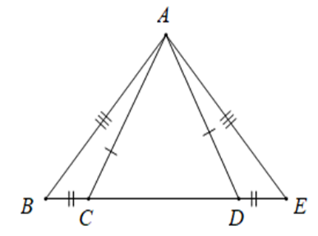
-
A.
\(\Delta ABC = \Delta {\rm E}DA\)
-
B.
\(\Delta ABC = \Delta EAD\)
-
C.
\(\Delta ABC = \Delta AED\)
-
D.
\(\Delta ABC = \Delta ADE\)
Lời giải và đáp án
Trên đường thẳng \(xy\) lấy hai điểm \(A,B\). Trên cùng nửa mặt phẳng bờ \(xy\) lấy hai điểm \(C\) và \(C'\) sao cho \(AC = BC';BC = AC'.\)
Chọn câu đúng.
-
A.
\(\widehat {BCA} = \widehat {BAC'}\)
-
B.
\(\Delta ACB = \Delta BAC'\)
-
C.
\(\widehat {BCA} = \widehat {ABC'}\)
-
D.
\(\Delta ACB = \Delta BC'A\)
Đáp án: D
Ta chứng minh hai tam giác bằng nhau theo trường hợp cạnh-cạnh-cạnh, sau đó suy ra hai góc tương ứng bằng nhau.
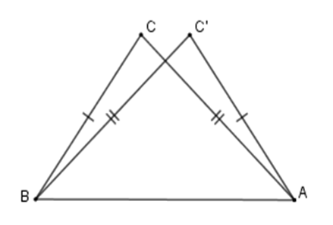
Hai tam giác \(ACB\) và \(BC'A\) có
$AC = BC'$ (gt)
\(BC = AC'\) (gt)
\(AB\) là cạnh chung
Nên \(\Delta ACB = \Delta BC'A\,\left( {c - c - c} \right).\)
Suy ra \(\widehat {BCA} = \widehat {BC'A}\) (hai góc tương ứng bằng nhau).
Nên A, B, C sai, D đúng.
So sánh hai góc \(\widehat {CAC'};\,\widehat {CBC'}\)?
-
A.
\(\widehat {CAC'} > \widehat {CBC'}\)
-
B.
\(\widehat {CAC'} < \widehat {CBC'}\)
-
C.
\(\widehat {CAC'} = \widehat {CBC'}\)
-
D.
\(\widehat {CAC'} = 2.\widehat {CBC'}\)
Đáp án: C
Ta chứng minh hai tam giác bằng nhau để suy ra hai góc tương ứng bằng nhau. Từ đó suy ra được điều phải chứng minh.
Vì \(\Delta ACB = \Delta BC'A\,\)(ý trước) ta suy ra \(\widehat {CAB} = \widehat {C'BA}\) và \(\widehat {C'AB} = \widehat {CBA}\) (1) (hai góc tương ứng bằng nhau)
Lại có \(\widehat {CAB} = \widehat {CAC'} + \widehat {C'AB}\) và \(\widehat {C'AB} = \widehat {CBC'} + \widehat {CBA}\) (tia làm giữa hai tia)
Suy ra $\widehat {CAC'} = \widehat {CAB} - \widehat {C'AB}$ và \(\widehat {CBC'} = \widehat {C'BA} - \widehat {CBA}\) (2)
Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(\widehat {CAC'} = \widehat {CBC'}\).
Cho \(\widehat {xOy} = {50^0}\), vẽ cung tròn tâm $O$ bán kính bằng $2cm,$ cung tròn này cắt $Ox, Oy$ lần lượt ở $A$ và $B.$ Vẽ các cung tròn tâm $A$ và tâm $B$ có bán kính $3cm,$ chúng cắt nhau tại điểm $C$ nằm trong góc $xOy.$ Tính \(\widehat {xOC}\) .
-
A.
\({25^0}\)
-
B.
\({50^0}\)
-
C.
\({80^0}\)
-
D.
\({90^0}\)
Đáp án : A
Ta chứng minh hai tam giác bằng nhau để suy ra hai góc tương ứng bằng nhau. Từ đó suy ra được điều phải chứng minh.
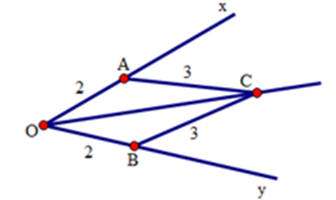
Xét hai tam giác $OAC$ và $OBC$ có:
$OA = OB = 2cm; OC$ là cạnh chung; $AC = BC = 3cm.$
Suy ra \(\Delta OAC = \Delta OBC(c.c.c)\)
Do đó \(\widehat {AOC} = \widehat {COB}\) (hai góc tương ứng).
Mà \(\widehat {AOC} + \widehat {COB} = {50^0}\) nên \(\widehat {AOC} = \widehat {COB} = \dfrac{{{{50}^0}}}{2} = {25^0}\)
Vậy \(\widehat {xOC} = {25^0}\).
Cho tam giác $ABC$ có $AB < AC$ . Gọi \(E \in AC\) sao cho \(AB = CE\). Gọi $O$ là một điểm nằm ở trong tam giác sao cho $OA = OC,OB = OE.$ Khi đó:
-
A.
\(\Delta AOB = \Delta CEO\)
-
B.
\(\Delta AOB = \Delta COE\)
-
C.
\(\widehat {AOB} = \widehat {OEC}\)
-
D.
\(\widehat {ABO} = \widehat {OCE}\)
Đáp án : B
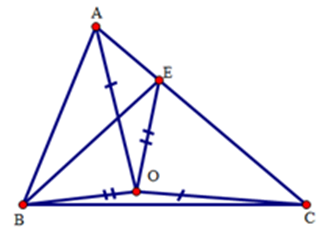
Xét tam giác $AOB$ và tam giác $COE$ có:
$AB = CE\,\left( {gt} \right);AO = CO\,(gt);OB = OE\,(gt)$
Do đó: \(\Delta AOB = \Delta COE(c.c.c)\) suy ra \(\widehat {AOB} = \widehat {COE};\,\widehat {ABO} = \widehat {OEC}\) (hai góc tương ứng bằng nhau)
Nên A, C, D sai, B đúng.
Cho tam giác $MNP$ có $MN = MP.$ Gọi $A$ là trung điểm của $NP.$ Biết \(\widehat {NMP} = {40^0}\) thì số đo góc $MPN$ là:
-
A.
\({100^0}\)
-
B.
\({70^0}\)
-
C.
\({80^0}\)
-
D.
\({90^0}\)
Đáp án : B
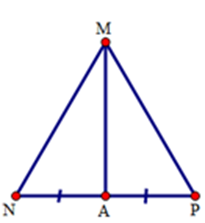
Xét tam giác $NAM$ và tam giác $PAM$ có:
$MN = MP,$ $NA = PA,$ $MA$ là cạnh chung. Do đó \(\Delta NAM = \Delta PAM\,\left( {c - c - c} \right).\)
Suy ra \(\widehat {ANM} = \widehat {APM}\) (hai góc tương ứng),
Ta có \(\widehat {ANM} = \widehat {APM}\)(cmt). Xét tam giác $MNP$ có:
\(\widehat {NMP} + \widehat {MPN} + \widehat {PNM} = {180^0} \Rightarrow 2\widehat {MPN} + \widehat {NMP} = {180^0}\)
\(\widehat {MPN} = \left( {{{180}^0} - \widehat {NMP}} \right):2 = \left( {{{180}^0} - {{40}^0}} \right):2 = {70^0}.\)
Cho tam giác $ABC$ có $AB = AC$ và $MB = MC$ (\(M \in BC\)). Chọn câu sai.
-
A.
$\Delta AMC = \Delta BCM$
-
B.
$AM \bot BC$
-
C.
\(\widehat {BAM} = \widehat {CAM}\)
-
D.
\(\Delta AMB = \Delta AMC\)
Đáp án : A
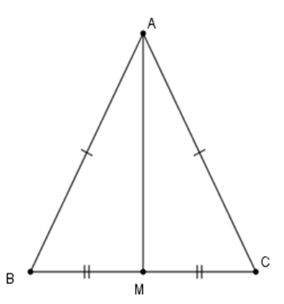
Xét \(\Delta AMB\) và \(\Delta AMC\) có
\(AB = AC\,\left( {gt} \right)\)
\(MB = MC\left( {gt} \right)\)
Cạnh \(AM\) chung
Nên \(\Delta AMB = \Delta AMC\,\left( {c - c - c} \right)\)
Suy ra \(\widehat {BAM} = \widehat {CAM}\) và $\widehat {AMB} = \widehat {AMC}$ (hai góc tương ứng bằng nhau) mà \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) (hai góc kề bù)
Nên $\widehat {AMB} = \widehat {AMC} = \dfrac{{180^\circ }}{2} = 90^\circ .$ Hay \(AM \bot BC.\)
Vậy B, C, D đúng, A sai.
Cho đoạn thẳng \(AB = 6cm.\) Trên một nửa mặt hẳng bờ $AB$ vẽ tam giác $ABC$ sao cho \(AC = 4cm,\) \(BC = 5cm,\) trên nửa mặt phẳng còn lại vẽ tam giác $ABD$ sao cho \(BD = 4cm,\) \(AD = 5cm.\) Chọn câu đúng.
-
A.
\(\Delta CAB = \Delta DAB\)
-
B.
\(\Delta ABC = \Delta BDA\)
-
C.
\(\Delta CAB = \Delta DBA\)
-
D.
\({\rm{\Delta CAB = \Delta {\rm A}{\rm B}D}}\)
Đáp án : C
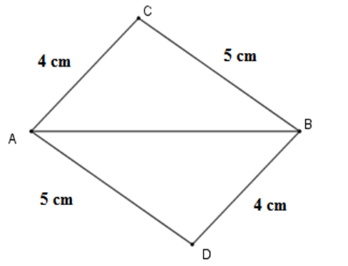
Từ bài ra ta có \(AC = BD = 4\,cm;\,BC = AD = 5\,cm.\)
Xét \(\Delta CAB\) và \(\Delta DBA\) có:
\(AC = BD\,\left( {cmt} \right)\)
\(BC = AD\,\left( {cmt} \right)\)
Cạnh \(AB\) chung
Nên \(\Delta CAB = \Delta DBA\,\left( {c - c - c} \right).\)
Cho tam giác $ABD$ và tam giác $IKH$ có $AB = KI,AD = KH,DB = IH.$
Phát biểu nào trong các phát biểu sau đây là đúng :
-
A.
\(\Delta BAD = \Delta HIK\)
-
B.
\(\Delta ABD = \Delta KHI\)
-
C.
\(\Delta DAB = \Delta HIK\)
-
D.
\(\Delta ABD = \Delta KIH\)
Đáp án: D
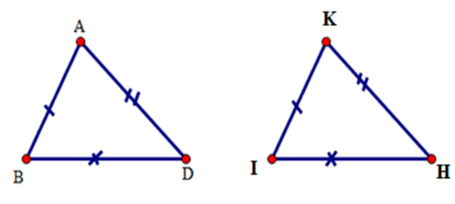
Xét tam giác $ABD$ và tam giác $KIH$ có:
$AB = KI,AD = KH,DB = IH.$
Do đó \(\Delta ABD = \Delta KIH\)(c.c.c).
Nếu \(\widehat A = {60^ \circ }\), thì số đo góc $K$ là:
-
A.
\({60^ \circ }\)
-
B.
\({70^ \circ }\)
-
C.
\({90^ \circ }\)
-
D.
\({120^ \circ }\)
Đáp án: A
Tính chất hai tam giác bằng nhau
Do \(\Delta ABD = \Delta KIH\) (theo câu trước), nên \(\widehat K = \widehat A = 60^\circ \) (hai góc tương ứng bằng nhau).
Cho hình dưới đây.

Chọn câu sai .
-
A.
\(AD//BC\)
-
B.
\(AB//CD\)
-
C.
\(\Delta ABC = \Delta CDA\)
-
D.
\(\Delta ABC = \Delta ADC\)
Đáp án : D
Dựa vào trường hợp bằng nhau thứ nhất của tam giác cạnh-cạnh-cạnh.
Sử dụng dấu hiệu nhận biết hai đường thẳng song song.
Xét tam giác \(ADC\) và \(CBA\) có
$AB = CD$
$AD = BC$
$DB$ chung
$ \Rightarrow \Delta ADC = CBA\left( {c.c.c} \right)$
Do đó \(\widehat {DAC} = \widehat {BCA}\) (hai góc tương ứng) mà hai góc ở vị trí so le trong nên \(AD//BC.\)
Tương tự ta có \(AB//DC.\)
Vậy A, B, C đúng, D sai.
Cho hai tam giác $ABD$ và $CDB$ có cạnh chung $BD.$ Biết $AB = DC$ và $AD = CB.$ Phát biểu nào sau đây là sai :
-
A.
\(\Delta ABC = \Delta CDA\)
-
B.
\(\widehat {ABC} = \widehat {CDA}\)
-
C.
\(\widehat {BAC} = \widehat {DAC}\)
-
D.
\(\widehat {BCA} = \widehat {DAC}\)
Đáp án : C
Dựa vào tính chất của hai tam giác bằng nhau.
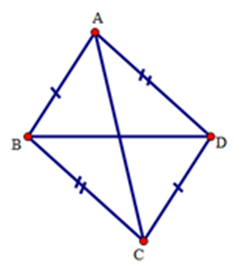
Xét \(\Delta ABC\) và \(\Delta CDA\) có:
\(AB = CD\left( {gt} \right)\)
\(BD{\rm{ chung}}\)
\(AD = BC\left( {gt} \right)\)
\( \Rightarrow \Delta ABC = \Delta CDA\left( {c.c.c} \right)\)
\( \Rightarrow \widehat {ABC} = \widehat {CDA},\widehat {BAC} = \widehat {DCA},\widehat {BCA} = \widehat {DAC}\) (góc tương ứng)
Vậy đáp án $C$ là sai.
Cho hình vẽ sau. Tam giác nào bằng với tam giác \(ABC?\)

-
A.
\(\Delta ABC = \Delta {\rm E}DA\)
-
B.
\(\Delta ABC = \Delta EAD\)
-
C.
\(\Delta ABC = \Delta AED\)
-
D.
\(\Delta ABC = \Delta ADE\)
Đáp án : C
Từ hình vẽ ta thấy \(AB = AE;\,BC = DE;\,AC = AD\) nên \(\Delta ABC = \Delta AED\,\left( {c - c - c} \right).\)