Trắc nghiệm Bài 5: Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh Toán 7 Cánh diều
Đề bài
Cho điểm \(A\) nằm trong góc nhọn \(xOy.\) Vẽ \(AH\) vuông góc với \(Ox,\) trên tia đối của tia \(HA\) lấy điểm \(B\) sao cho \(HB = HA.\) Vẽ \(AK\) vuông góc với \(Oy,\) trên tia đổi của tia \(KA\) lấy điểm \(C\) sao cho \(KC = KA.\)
So sánh \(OB;OC\).
-
A.
\(OB < OC\)
-
B.
\(OB = OC\)
-
C.
\(OB > OC\)
-
D.
\(OB \ge OC\)
Biết \(\widehat {xOy} = \alpha .\) Tính \(\widehat {BOC}.\)
-
A.
\(3\alpha \)
-
B.
\(4\alpha \)
-
C.
\(2\alpha \)
-
D.
\(\alpha \)
Cho tam giác \(ABC\) vuông tại \(A.\) Tia phân giác của góc \(ABC\) cắt \(AC\) tại \(D,\) lấy \(E\) trên cạnh \(BC\) sao cho \(BE = AB.\)
Chọn câu đúng.
-
A.
\(\Delta ABD{\rm{ }} = \Delta EBD\)
-
B.
\(\Delta ABD{\rm{ }} = \Delta BED\)
-
C.
\(DC = DE\)
-
D.
\(\Delta ABD = \Delta CBD\)
Trên tia đối của tia \(DE\) lấy điểm \(M\) sao cho \(DM = DC\). So sánh \(EC\) và \(AM\).
-
A.
\(EC < AM\)
-
B.
\(EC = AM\)
-
C.
\(EC > AM\)
-
D.
Chưa đủ điều kiện để so sánh
Trên tia đối của tia \(DE\) lấy điểm \(M\) sao cho \(DM = DC\). Nối \(AE,\) so sánh số đo \(\widehat {AEC};\widehat {EAM}\).
-
A.
\(\widehat {AEC} > \widehat {EAM}\)
-
B.
\(\widehat {AEC} < \widehat {EAM}\)
-
C.
\(\widehat {AEC} = \widehat {EAM}\)
-
D.
Chưa đủ điều kiện so sánh
Cho tam giác \(ABC\) có \(\widehat A = {90^0},M\) là trung điểm \(AC.\) Trên tia đối của tia \(MB\) lấy \(K\) sao cho \(MK = MB.\) Chọn câu đúng nhất :
-
A.
\(KC \bot AC\)
-
B.
\(AK//BC\)
-
C.
\(AK = CB\)
-
D.
Cả A, B, C đều đúng
Cho hai đoạn thẳng \(AB\) và \(CD\) cắt nhau tại \(O\) là trung điểm của mỗi đoạn thẳng đó. Lấy \(E;\,F\) lần lượt là điểm thuộc đoạn \(AD\) và \(BC\) sao cho \(AE = BF.\) Cho \(OE = 2cm\), tính \(EF.\)
-
A.
\(4\,cm\)
-
B.
\(2cm\)
-
C.
$3\,cm$
-
D.
\(3,5\,cm\)
Cho tam giác $ABC$ có $M,N$ lần lượt là trung điểm của $AB,AC.$ Trên tia đối của tia $MC$ lấy $D$ sao cho $MD = MC$ . Trên tia đối của tia $NB$ lấy điểm $E$ sao cho $NE = NB.$
(I) \(\Delta AMD = \Delta BMC\)
(II) \(\Delta ANE = \Delta CNB\)
(III) $A,D,E$ thẳng hàng
(IV) $A$ là trung điểm của đoạn thẳng $DE$
Số khẳng định đúng trong các khẳng định trên là
-
A.
\(0\)
-
B.
\(2\)
-
C.
$4$
-
D.
\(3\)
Cho góc nhọn $xOy$ và $Oz$ là tia phân giác của góc đó. Trên tia $Ox$ lấy điểm $A$ và trên tia $Oy$ lấy điểm $B$ sao cho $OA = OB.$ Gọi $C$ là một điểm bất kỳ trên tia $Oz.$
Chọn câu sai.
-
A.
\(AC = OB\)
-
B.
\(AC = BC\)
-
C.
\(\widehat {OAC} = \widehat {OBC}\)
-
D.
\(CO\) là tia phân giác của \(\widehat {BCA}.\)
Gọi \(I\) là giao của \(AB\) và \(Oz.\) Tính góc \(AIC.\)
-
A.
\(120^\circ \)
-
B.
\(90^\circ \)
-
C.
$60^\circ $
-
D.
\({100^0}\)
Cho tam giác $ABC$ có $AB = AC = BC,$ phân giác $BD$ và $CE$ cắt nhau tại $O.$
Chọn câu đúng.
-
A.
$CE \bot \;AB$
-
B.
$BD\; \bot AC$
-
C.
\(DC = BC\)
-
D.
Cả A, B đều đúng.
Tính \(\widehat {BOC}.\)
-
A.
\({60^0}\)
-
B.
\({80^0}\)
-
C.
$120^\circ $
-
D.
\({100^0}\)
Cho đoạn thẳng \(AB\), trên đường trung trực \(d\) của đoạn \(AB\) lấy điểm \(M.\) So sánh \(AM\) và \(BM.\)
-
A.
\(MA = MB\)
-
B.
\(MA > MB\)
-
C.
\(MA < MB\)
-
D.
\(2.MA = MB\)
Cho tam giác $ABC$ có \(\widehat A = {90^0}\), tia phân giác $BD$ của góc $B$ (\(D \in AC\)). Trên cạnh $BC$ lấy điểm $E$ sao cho $BE = BA.$ Hai góc nào sau đây bằng nhau?
-
A.
\(\widehat {EDC};\widehat {BAC}\)
-
B.
\(\widehat {EDC};\widehat {ACB}\)
-
C.
\(\widehat {EDC};\widehat {ABC}\)
-
D.
\(\widehat {EDC};\widehat {EC{\rm{D}}}\)
Cho tam giác $DEF$ và tam giác $HKG$ có $DE = HK$ , \(\widehat E = \widehat K\), $EF = KG.$ Biết \(\widehat D = {70^0}\). Số đo góc $H$ là:
-
A.
\({70^0}\)
-
B.
\({80^0}\)
-
C.
\({90^0}\)
-
D.
\({100^0}\)
Cho góc nhọn $xOy.$ Trên tia $Ox$ lấy hai điểm $A,C,$ trên tia $Oy$ lấy hai điểm $B,D$ sao cho $OA = OB,OC = OD$ ($A$ nằm giữa $O$ và $C,$$B$ nằm giữa $O$ và $D$ ).
Chọn câu đúng.
-
A.
\(\Delta OAD = \Delta OCB\)
-
B.
\(\Delta ODA = \Delta OBC\)
-
C.
\(\Delta AOD = \Delta BCO\)
-
D.
\(\Delta OAD = \Delta OBC\) .
So sánh hai góc \(\widehat {CAD}\) và \(\widehat {CBD}.\)
-
A.
\(\widehat {CBD} = \widehat {CAD}\)
-
B.
\(\widehat {CBD} < \widehat {CAD}\)
-
C.
\(\widehat {CBD} > \widehat {CAD}\)
-
D.
\(\widehat {CBD} =2.\widehat {CAD}\) .
Cho hai đoạn thẳng $BD$ và $EC$ vuông góc với nhau tại $A$ sao cho $AB = AE,AD = AC,AB < AC.$ Phát biểu nào trong các phát biểu sau đây là sai:
-
A.
\(\Delta AED = \Delta ABC\)
-
B.
$BC = ED$
-
C.
$EB = CD$
-
D.
\(\widehat {ABC} = \widehat {AED}\) .
Cho tam giác $BAC$ và tam giác $KEF$ có $BA = EK,$ \(\widehat A = \widehat K\), $CA = KF.$ Phát biểu nào trong trong các phát biểu sau đây là đúng :
-
A.
\(\Delta BAC = \Delta EKF\)
-
B.
\(\Delta BAC = \Delta EFK\)
-
C.
\(\Delta {\rm A}BC = \Delta FKE\)
-
D.
\(\Delta BAC = \Delta KEF\)
Cho tam giác $ABC$ và tam giác $MHK$ có: $AB = MH$ , \(\widehat A = \widehat M\). Cần thêm một điều kiện gì để hai tam giác $ABC$ và $MHK$ bằng nhau theo trường hợp cạnh – góc – cạnh:
-
A.
$BC = MK$
-
B.
$BC = HK$
-
C.
$AC = MK$
-
D.
$AC = HK$
Lời giải và đáp án
Cho điểm \(A\) nằm trong góc nhọn \(xOy.\) Vẽ \(AH\) vuông góc với \(Ox,\) trên tia đối của tia \(HA\) lấy điểm \(B\) sao cho \(HB = HA.\) Vẽ \(AK\) vuông góc với \(Oy,\) trên tia đổi của tia \(KA\) lấy điểm \(C\) sao cho \(KC = KA.\)
So sánh \(OB;OC\).
-
A.
\(OB < OC\)
-
B.
\(OB = OC\)
-
C.
\(OB > OC\)
-
D.
\(OB \ge OC\)
Đáp án: B
Sử dụng trường hợp bằng nhau thứ hai của tam giác để chứng minh \(\Delta OAH = \Delta OBH\), \(\Delta OAK = \Delta OCK\). Từ đó suy ra các cạnh tương ứng bằng nhau.
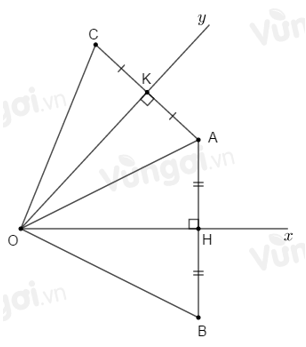
Xét \(\Delta OAH\) và \(\Delta OBH\) có:
\(OH\) cạnh chung
\(\widehat {OHA} = \widehat {OHB} = {90^o}\)
\(HA = HB\,(gt)\)
\( \Rightarrow \Delta OAH = \Delta OBH\,(c.g.c)\)
\( \Rightarrow OA = OB\) (hai cạnh tương ứng) (1)
Xét \(\Delta OAK\) và \(\Delta OCK\) có:
\(OK\) cạnh chung
\(\widehat {OKA} = \widehat {OKC} = {90^o}\)
\(KA = KC\,(gt)\)
\( \Rightarrow \Delta OAK = \Delta OCK\,(c.g.c)\)
\( \Rightarrow OA = OC\) (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra \(OA = OB = OC.\)
Biết \(\widehat {xOy} = \alpha .\) Tính \(\widehat {BOC}.\)
-
A.
\(3\alpha \)
-
B.
\(4\alpha \)
-
C.
\(2\alpha \)
-
D.
\(\alpha \)
Đáp án: C
Sử dụng kết quả câu trước ta có: \(\Delta OAH = \Delta OBH\), \(\Delta OAK = \Delta OCK\). Từ đó suy ra \(\widehat {BOH} = \widehat {AOH}\), \(\widehat {AOK} = \widehat {COK}\) (các cặp góc tương ứng), sau đó biến đổi để tìm được số đo của \(\widehat {BOC}.\)
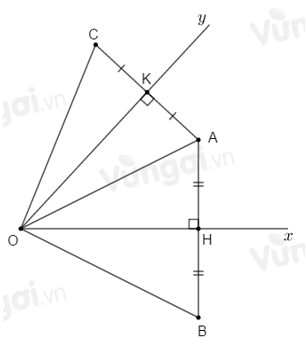
Sử dụng kết quả câu trước ta có: \(\Delta OAH = \Delta OBH\), \(\Delta OAK = \Delta OCK\).
Vì \(\Delta OAH = \Delta OBH\) suy ra \(\widehat {BOH} = \widehat {AOH}\) (hai góc tương ứng).
Vì \(\Delta OAK = \Delta OCK\) suy ra \(\widehat {AOK} = \widehat {COK}\) (hai góc tương ứng).
Ta có \(\widehat {BOC} = \widehat {BOA} + \widehat {AOC}\)
\( \Rightarrow \widehat {BOC} = \widehat {BOH} + \widehat {AOH} + \widehat {AOK} + \widehat {COK}\)
\( \Rightarrow \widehat {BOC} = 2\widehat {AOH} + 2\widehat {AOK}\) (vì \(\widehat {BOH} = \widehat {AOH}\) và \(\widehat {AOK} = \widehat {COK}\))
\( \Rightarrow \widehat {BOC} = 2\left( {\widehat {AOH} + \widehat {AOK}} \right) = 2\widehat {xOy} = 2\alpha .\)
Cho tam giác \(ABC\) vuông tại \(A.\) Tia phân giác của góc \(ABC\) cắt \(AC\) tại \(D,\) lấy \(E\) trên cạnh \(BC\) sao cho \(BE = AB.\)
Chọn câu đúng.
-
A.
\(\Delta ABD{\rm{ }} = \Delta EBD\)
-
B.
\(\Delta ABD{\rm{ }} = \Delta BED\)
-
C.
\(DC = DE\)
-
D.
\(\Delta ABD = \Delta CBD\)
Đáp án: A
Sử dụng trường hợp bằng nhau thứ hai của tam giác để chứng minh \(\Delta ABD{\rm{ }} = \Delta EBD\).
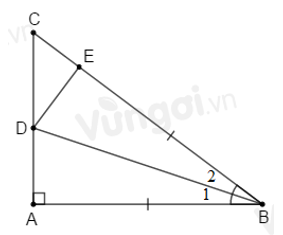
Xét \(\Delta ABD\) và \(\Delta EBD\) có:
\(BA = BE\) (gt)
\(\widehat {{B_1}} = \widehat {{B_2}}\) (vì \(BD\) là tia phân giác \(\widehat {ABC}\))
\(BD\) cạnh chung
\( \Rightarrow \Delta ABD{\rm{ }} = \Delta EBD\,(c.g.c)\)
Trên tia đối của tia \(DE\) lấy điểm \(M\) sao cho \(DM = DC\). So sánh \(EC\) và \(AM\).
-
A.
\(EC < AM\)
-
B.
\(EC = AM\)
-
C.
\(EC > AM\)
-
D.
Chưa đủ điều kiện để so sánh
Đáp án: B
- Sử dụng kết quả câu trước \(\Delta ABD{\rm{ }} = \Delta EBD\) suy ra \(DE = DA\) (hai cạnh tương ứng).
- Sử dụng trường hợp bằng nhau thứ hai của tam giác để chứng minh \(\Delta ADM = \Delta EDC\) từ đó suy ra điều phải chứng minh.
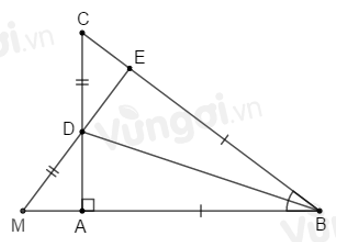
Sử dụng kết quả câu trước \(\Delta ABD{\rm{ }} = \Delta EBD\) suy ra \(DE = DA\) (hai cạnh tương ứng). Nối \(AM.\)
Xét \(\Delta ADM\) và \(\Delta EDC\) có:
\(DA = DE\) (chứng minh trên)
\(\widehat {ADM} = \widehat {EDC}\) (hai góc đối đỉnh)
\(DM = DC\,(gt)\)
\( \Rightarrow \Delta ADM = \Delta EDC\,(c.g.c)\)
\( \Rightarrow AM = EC\) (hai cạnh tương ứng bằng nhau).
Trên tia đối của tia \(DE\) lấy điểm \(M\) sao cho \(DM = DC\). Nối \(AE,\) so sánh số đo \(\widehat {AEC};\widehat {EAM}\).
-
A.
\(\widehat {AEC} > \widehat {EAM}\)
-
B.
\(\widehat {AEC} < \widehat {EAM}\)
-
C.
\(\widehat {AEC} = \widehat {EAM}\)
-
D.
Chưa đủ điều kiện so sánh
Đáp án: C
- Sử dụng kết quả câu trước \(\Delta ADM = \Delta EDC\) suy ra \(AD = ED;\,AM = EC\) (các cạnh tương ứng).
- Sử dụng trường hợp bằng nhau thứ nhất của tam giác để chứng minh \(\Delta AEC = \Delta EAM\), từ đó suy ra điều phải chứng minh.
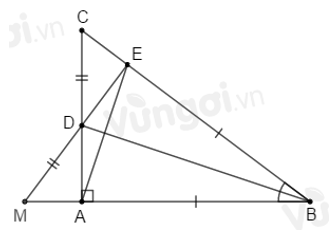
Sử dụng kết quả câu trước \(\Delta ADM = \Delta EDC\) suy ra \(AD = ED;\,AM = EC\) (các cạnh tương ứng).
Ta có: \(AD = ED\,\,\,\,(1)\)
\(DC = DM\,\,\,(2)\)
Cộng (1) và (2) theo vế với vế ta được: \(AD + DC = ED + DM\) hay \(AC = EM\).
Xét \(\Delta AEC\) và \(\Delta EAM\) có:
\(AE\) cạnh chung
\(EC = AM\,(cmt)\)
\(AC = EM\,(cmt)\)
\( \Rightarrow \Delta AEC = \Delta EAM\,(c.c.c)\)
\( \Rightarrow \widehat {AEC} = \widehat {EAM}\) (hai góc tương ứng).
Cho tam giác \(ABC\) có \(\widehat A = {90^0},M\) là trung điểm \(AC.\) Trên tia đối của tia \(MB\) lấy \(K\) sao cho \(MK = MB.\) Chọn câu đúng nhất :
-
A.
\(KC \bot AC\)
-
B.
\(AK//BC\)
-
C.
\(AK = CB\)
-
D.
Cả A, B, C đều đúng
Đáp án : D
Sử dụng trường hợp bằng nhau thứ hai của tam giác để chứng minh \(\Delta ABM = \Delta CKM\) và \(\Delta AMK = \Delta CMB\), từ đó suy ra các góc tương ứng bằng nhau và lí luận để suy ra điều phải chứng minh.
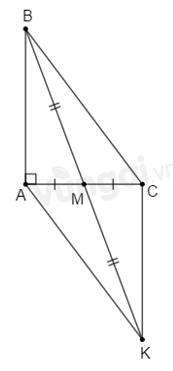
Xét \(\Delta ABM\) và \(\Delta CKM\) có:
\(AM = CM\) (vì \(M\) là trung điểm \(AC\))
\(MB = MK\,\,(gt)\)
\(\widehat {AMB} = \widehat {CMK}\) (hai góc đối đỉnh)
\( \Rightarrow \Delta ABM = \Delta CKM\,\,(c.g.c)\)
\( \Rightarrow \widehat {BAM} = \widehat {KCM}\) (hai góc tương ứng).
Mà \(\widehat {BAM} = {90^o}\) (vì \(\Delta ABC\) vuông tại \(A\)) suy ra \(\widehat {KCM} = {90^o}\).
Do đó \(KC \bot AC\) (A đúng).
Xét \(\Delta AMK\) và \(\Delta CMB\) có:
\(AM = CM\) (vì \(M\) là trung điểm \(AC\))
\(MK = MB\,\,(gt)\)
\(\widehat {AMK} = \widehat {CMB}\) (hai góc đối đỉnh)
\( \Rightarrow \Delta AMK = \Delta CMB\,(c.g.c)\)
\( \Rightarrow AK = CB\) (hai cạnh tương ứng) (C đúng).
\( \Rightarrow \widehat {MAK} = \widehat {MCB}\) (hai góc tương ứng).
Mà \(\widehat {MAK}\) và \(\widehat {MCB}\) ở vị trí so le trong nên \(AK//BC\) (B đúng).
Cho hai đoạn thẳng \(AB\) và \(CD\) cắt nhau tại \(O\) là trung điểm của mỗi đoạn thẳng đó. Lấy \(E;\,F\) lần lượt là điểm thuộc đoạn \(AD\) và \(BC\) sao cho \(AE = BF.\) Cho \(OE = 2cm\), tính \(EF.\)
-
A.
\(4\,cm\)
-
B.
\(2cm\)
-
C.
$3\,cm$
-
D.
\(3,5\,cm\)
Đáp án : A
Dùng trường hợp bằng nhau thứ hai để chứng minh hai tam giác bằng nhau, từ đó có các cạnh và các góc tương ứng. Lập luận để có được \(O\) là trung điểm của \(EF\) để tính độ dài \(EF.\)
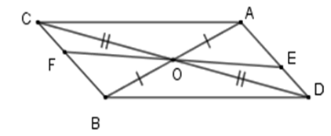
* Xét tam giác \(OBC\) và \(OAD\) có
+ \(OA = OB\,\left( {gt} \right)\)
+ \(\widehat {AOD} = \widehat {BOC}\) (đối đỉnh)
+ \(OC = OD\left( {gt} \right)\)
Suy ra \(\Delta OAD = \Delta OBC\left( {c - g - c} \right)\) nên \(\widehat {OAD} = \widehat {OBC}\) (hai góc tương ứng)
* Xét tam giác \(OBF\) và \(OAE\) có
+ \(OA = OB\,\left( {gt} \right)\)
+ \(\widehat {OAD} = \widehat {OBC}\) (cmt)
+ \(BF = AE\left( {gt} \right)\)
Suy ra \(\Delta OBF = \Delta OAE\left( {c - g - c} \right)\) nên \(OE = OF\) (hai cạnh tương ứng) và \(\widehat {AOE} = \widehat {FOB}\) (hai góc tương ứng)
Mà \(\widehat {FOB} + \widehat {FOA} = 180^\circ \) (hai góc kề bù) nên \(\widehat {FOA} + \widehat {AOE} = 180^\circ \)
Suy ra ba điểm \(F;\,O;E\) thẳng hàng và \(OE = OF\) nên \(O\) là trung điểm của \(EF \Rightarrow EF = 2.OE = 4\,cm.\)
Cho tam giác $ABC$ có $M,N$ lần lượt là trung điểm của $AB,AC.$ Trên tia đối của tia $MC$ lấy $D$ sao cho $MD = MC$ . Trên tia đối của tia $NB$ lấy điểm $E$ sao cho $NE = NB.$
(I) \(\Delta AMD = \Delta BMC\)
(II) \(\Delta ANE = \Delta CNB\)
(III) $A,D,E$ thẳng hàng
(IV) $A$ là trung điểm của đoạn thẳng $DE$
Số khẳng định đúng trong các khẳng định trên là
-
A.
\(0\)
-
B.
\(2\)
-
C.
$4$
-
D.
\(3\)
Đáp án : C
(I), (II) Dựa vào trường hợp bằng nhau thứ hai của tam giác để chứng minh các tam giác bằng nhau
(III) Để chứng minh ba điểm $A,D,E$ thẳng hàng ta chứng minh $A$ có hai đường thẳng $AD,AE$ cùng song song với $BC.$
(IV) Để chứng minh $A$ là trung điểm của $DE$ ta chứng minh $AD$ và $AE$ cùng bằng $BC$ do đó chúng bằng nhau.
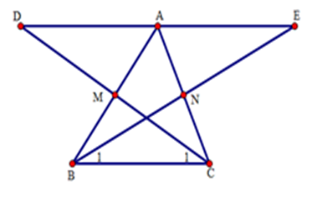
(I) Xét \(\Delta AMD\) và \(\Delta BMC\) có: $DM = MC\left( {gt} \right);$ \(\widehat {BMC} = \widehat {AMD}\) (hai góc đối đỉnh); $AM = BM\left( {gt} \right),$ nên \(\Delta AMD = \Delta BMC\)(c.g.c).
(II) Xét \(\Delta ANE\) và \(\Delta CNB\) có: $AN = NC\left( {gt} \right);$ \(\widehat {ANE} = \widehat {CNB}\)(hai góc đối đỉnh), $NB = NE\left( {gt} \right),$ do đó
\(\Delta CNB = \Delta ANE\)(c.g.c).
(III) Do \(\Delta AMD = \Delta BMC\) nên \(\widehat D = \widehat {{C_1}}\)(hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên $AD//BC.$
Do \(\Delta CNB = \Delta ANE\)nên \(\widehat E = \widehat {{B_1}}\)(hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên $AE//BC.$
Như vậy qua $A$ có hai đường thẳng $AD,AE$ cùng song song với $BC.$
Do đó $D,A,E$ thẳng hàng. (1)
(IV) Ta có: $AD = BC$ (do \(\Delta AMD = \Delta BMC\)); $AE = BC$ (do \(\Delta CNB = \Delta ANE\)) nên $AD = AE\left( 2 \right)$
Từ (1) và (2) suy ra $A$ là trung điểm của $DE.$
Vậy cả (I); (II); (III); (IV) đều đúng.
Cho góc nhọn $xOy$ và $Oz$ là tia phân giác của góc đó. Trên tia $Ox$ lấy điểm $A$ và trên tia $Oy$ lấy điểm $B$ sao cho $OA = OB.$ Gọi $C$ là một điểm bất kỳ trên tia $Oz.$
Chọn câu sai.
-
A.
\(AC = OB\)
-
B.
\(AC = BC\)
-
C.
\(\widehat {OAC} = \widehat {OBC}\)
-
D.
\(CO\) là tia phân giác của \(\widehat {BCA}.\)
Đáp án: A
Chứng minh hai tam giác bằng nhau theo trường hợp thứ hai và tính chất hai tam giác bằng nhau.
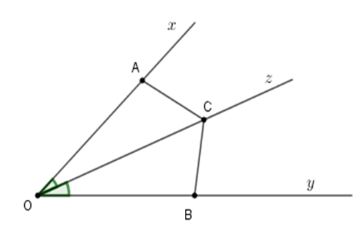
Xét tam giác \(AOC\) và \(BOC\) có
+ \(OA = OB\left( {gt} \right)\)
+ \(\widehat {AOC} = \widehat {BOC}\) (tính chất tia phân giác)
+ Cạnh $OC$ chung
Suy ra \(\Delta AOC = \Delta BOC\left( {c - g - c} \right)\)
\( \Rightarrow AC = BC\) (hai cạnh tương ứng); \(\widehat {OAC} = \widehat {OBC}\); \(\widehat {OCA} = \widehat {OCB}\) (hai góc tương ứng)
Từ đó \(CO\) là tia phân giác của \(\widehat {BCA}.\)
Nên B, C, D đúng, A sai.
Gọi \(I\) là giao của \(AB\) và \(Oz.\) Tính góc \(AIC.\)
-
A.
\(120^\circ \)
-
B.
\(90^\circ \)
-
C.
$60^\circ $
-
D.
\({100^0}\)
Đáp án: B
Sử dụng trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh
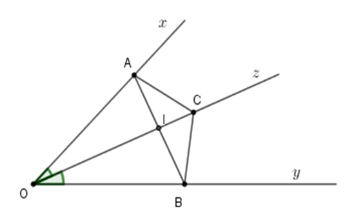
Xét tam giác \(AOI\) và \(BOI\) có
+ \(OA = OB\left( {gt} \right)\)
+ \(\widehat {AOI} = \widehat {BOI}\) (tính chất tia phân giác)
+ Cạnh $OI$ chung
Suy ra \(\Delta AOI = \Delta BOI\left( {c - g - c} \right)\)
Do đó \(\widehat {AIO} = \widehat {BIO}\) (hai góc tương ứng) mà \(\widehat {AIO} + \widehat {BIO} = 180^\circ \) nên \(\widehat {AIO} = \widehat {BIO} = \dfrac{{180^\circ }}{2} = 90^\circ \)
Hay \(OC \bot AB \Rightarrow \widehat {AIC} = 90^\circ .\)
Cho tam giác $ABC$ có $AB = AC = BC,$ phân giác $BD$ và $CE$ cắt nhau tại $O.$
Chọn câu đúng.
-
A.
$CE \bot \;AB$
-
B.
$BD\; \bot AC$
-
C.
\(DC = BC\)
-
D.
Cả A, B đều đúng.
Đáp án: D
Dựa vào tính chất hai tam giác bằng nhau và tính chất hai góc kề bù.
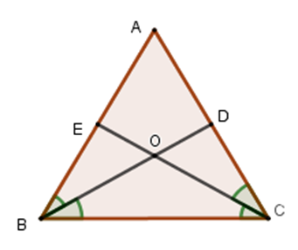
Vì \(BD\) và \(CE\) là tia phân giác của góc \(\widehat {ABC}\) và \(\widehat {ACB}\) nên \(\widehat {ABD} = \widehat {CBD}\) và \(\widehat {ACE} = \widehat {BCE}.\)
Xét tam giác \(ABD\) và tam giác \(CBD\) có:
+ \(AB = AC\,\left( {gt} \right)\)
+ \(\widehat {ABD} = \widehat {CBD}\) (cmt)
+ Cạnh \(BD\) chung
Suy ra \(\Delta ABD = \Delta CBD\,\left( {c - g - c} \right)\)
\( \Rightarrow \widehat {ADB} = \widehat {BDC}\) (hai góc tương ứng); \(DC = AD\) (hai cạnh tương ứng) nên C sai.
Mà \(\widehat {ADB} + \widehat {CDB} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {ADB} = \widehat {CDB} = \dfrac{{180^\circ }}{2} = 90^\circ \) . Do đó \(BD \bot AC.\)
Tương tự ta có \(CE \bot AB.\)
Tính \(\widehat {BOC}.\)
-
A.
\({60^0}\)
-
B.
\({80^0}\)
-
C.
$120^\circ $
-
D.
\({100^0}\)
Đáp án: C
Sử dụng tính chất tia phân giác, tính chất hai góc kề bù và định lý tổng ba góc trong tam giác.
Từ câu trước ta có \(\Delta ABD = \Delta CBD\,\left( {c - g - c} \right)\)\( \Rightarrow \widehat {BCA} = \widehat {BAC}\) (hai góc tương ứng) (1)
Tương tự ta có \(\Delta BCE = \Delta ACE\left( {c - g - c} \right)\) \( \Rightarrow \widehat {CBA} = \widehat {BAC}\) (hai góc tương ứng) (2)
Từ (1) và (2) ta có \(\widehat {ABC} = \widehat {BAC} = \widehat {ACB}\). Mà \(\widehat {ABC} + \widehat {BAC} + \widehat {ACB} = 180^\circ \) (định lý tổng ba góc của tam giác) nên \(\widehat {ABC} = \widehat {BAC} = \widehat {ACB} = \dfrac{{180^\circ }}{3} = 60^\circ .\)
Lại có \(\widehat {ABD} = \widehat {CBD}\) (cmt) nên \(\widehat {CBO} = \dfrac{{\widehat {ABC}}}{2} = \dfrac{{60^\circ }}{2} = 30^\circ \); \(\widehat {ACE} = \widehat {BCE} = \dfrac{{\widehat {ACB}}}{2} = \dfrac{{60^\circ }}{2} = 30^\circ .\)
Xét tam giác \(BOC\) có \(\widehat {BOC} + \widehat {OBC} + \widehat {OCB} = 180^\circ \) (định lý tổng ba góc của một tam giác)
Nên \(\widehat {BOC} = 180^\circ - 30^\circ - 30^\circ = 120^\circ .\)
Vậy \(\widehat {BOC} = 120^\circ .\)
Cho đoạn thẳng \(AB\), trên đường trung trực \(d\) của đoạn \(AB\) lấy điểm \(M.\) So sánh \(AM\) và \(BM.\)
-
A.
\(MA = MB\)
-
B.
\(MA > MB\)
-
C.
\(MA < MB\)
-
D.
\(2.MA = MB\)
Đáp án : A
Sử dụng hai tam giác bằng nhau theo trường hợp cạnh-cạnh-cạnh từ đó suy ra \(AM = BM.\)
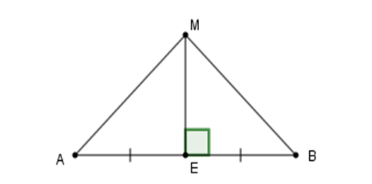
Đường trung trực của \(AB\) vuông góc với \(AB\) tại trung điểm \(E\) . Do đó \(ME \bot AB;\,EA = EB.\)
Xét tam giác \(MEA\) và tam giác \(MEB\) có \(EA = EB\,\left( {cmt} \right),\) \(\widehat {MEA} = \widehat {MEB} = 90^\circ ,\) cạnh \(ME\) chung nên \(\Delta MEA = \Delta MEB\,\left( {c - g - c} \right)\) suy ra \(MA = MB\) (hai cạnh tương ứng).
Cho tam giác $ABC$ có \(\widehat A = {90^0}\), tia phân giác $BD$ của góc $B$ (\(D \in AC\)). Trên cạnh $BC$ lấy điểm $E$ sao cho $BE = BA.$ Hai góc nào sau đây bằng nhau?
-
A.
\(\widehat {EDC};\widehat {BAC}\)
-
B.
\(\widehat {EDC};\widehat {ACB}\)
-
C.
\(\widehat {EDC};\widehat {ABC}\)
-
D.
\(\widehat {EDC};\widehat {EC{\rm{D}}}\)
Đáp án : C
Sử dụng trường hợp bằng nhau thứ hai của tam giác để suy ra \(\widehat {BED} = \widehat {BAD} = 90^\circ \) và lập luận để chỉ ra \(\widehat {EDC} = \widehat {ABC}.\)
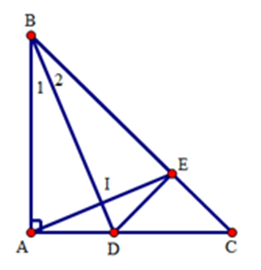
Xét hai tam giác $BDA$ và $BDE$ có:$BA = BE\left( {gt} \right),$ \(\widehat {{B_1}} = \widehat {{B_2}}\) (do $BD$ là tia phân giác của góc B);
$BD$ là cạnh chung. Suy ra \(\Delta BDA = \Delta BDE\) (c.g.c)
Suy ra \(\widehat {BED} = \widehat {BAD} = {90^ \circ }\) (hai góc tương ứng)
Trong các tam giác $ABC$ và $EDC$ vuông ở $A$ và $E,$ ta có:
\(\widehat {ABC} + \widehat C = {90^ \circ }\) và \(\widehat {EDC} + \widehat C = {90^ \circ }\), suy ra \(\widehat {EDC} = \widehat {ABC}\).
Cho tam giác $DEF$ và tam giác $HKG$ có $DE = HK$ , \(\widehat E = \widehat K\), $EF = KG.$ Biết \(\widehat D = {70^0}\). Số đo góc $H$ là:
-
A.
\({70^0}\)
-
B.
\({80^0}\)
-
C.
\({90^0}\)
-
D.
\({100^0}\)
Đáp án : A
+Sử dụng trường hợp bằng nhau thứ hai của tam giác để chứng minh hai tam giác bằng nhau từ đó suy ra hai góc tương ứng bằng nhau.
Xét tam giác $DEF$ và tam giác $HKG$ có $DE = HK$ , \(\widehat E = \widehat K\), $EF = KG.$
do đó \(\Delta DEF = \Delta HKG\) (c.g.c).
Do đó \(\widehat H = \widehat D = {70^0}\) (hai góc tương ứng).
Cho góc nhọn $xOy.$ Trên tia $Ox$ lấy hai điểm $A,C,$ trên tia $Oy$ lấy hai điểm $B,D$ sao cho $OA = OB,OC = OD$ ($A$ nằm giữa $O$ và $C,$$B$ nằm giữa $O$ và $D$ ).
Chọn câu đúng.
-
A.
\(\Delta OAD = \Delta OCB\)
-
B.
\(\Delta ODA = \Delta OBC\)
-
C.
\(\Delta AOD = \Delta BCO\)
-
D.
\(\Delta OAD = \Delta OBC\) .
Đáp án: D
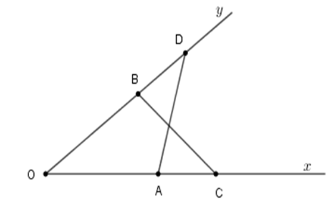
Xét tam giác \(OAD\) và tam giác \(OBC\) có
$OA = OB,$ góc \(O\) chung, $OD = OC$ suy ra \(\Delta OAD = \Delta OBC\,\left( {c - g - c} \right).\)
So sánh hai góc \(\widehat {CAD}\) và \(\widehat {CBD}.\)
-
A.
\(\widehat {CBD} = \widehat {CAD}\)
-
B.
\(\widehat {CBD} < \widehat {CAD}\)
-
C.
\(\widehat {CBD} > \widehat {CAD}\)
-
D.
\(\widehat {CBD} =2.\widehat {CAD}\) .
Đáp án: A
Sử dụng tính chất hai tam giác bằng nhau ở ý trước suy ra hai góc tương ứng bằng nhau
Sau đó sử dụng tính chất hai góc kề bù hoặc góc ngoài để so sánh hai góc \(\widehat {CAD}\) và \(\widehat {CBD}.\)
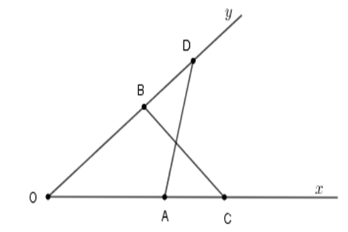
Vì \(\Delta OAD = \Delta OBC\,\left( {c - g - c} \right).\) Suy ra \(\widehat {OBC} = \widehat {OAD}\) (hai góc tương ứng bằng nhau)
Lại có \(\widehat {OBC} + \widehat {CBD} = 180^\circ ;\,\widehat {OAD} + \widehat {DAC} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {CBD} = 180^\circ - \widehat {OBC}\) và \(\widehat {CAD} = 180^\circ - \widehat {OAD}\) mà \(\widehat {OBC} = \widehat {OAD}\) (cmt)
Suy ra \(\widehat {CBD} = \widehat {CAD}.\)
Cho hai đoạn thẳng $BD$ và $EC$ vuông góc với nhau tại $A$ sao cho $AB = AE,AD = AC,AB < AC.$ Phát biểu nào trong các phát biểu sau đây là sai:
-
A.
\(\Delta AED = \Delta ABC\)
-
B.
$BC = ED$
-
C.
$EB = CD$
-
D.
\(\widehat {ABC} = \widehat {AED}\) .
Đáp án : C
+Sử dụng trường hợp bằng nhau thứ hai của tam giác để chứng minh hai tam giác bằng nhau.
+Sử dụng tính chất của hai tam giác bằng nhau để suy ra các tính chất về cạnh, về góc tương ứng.
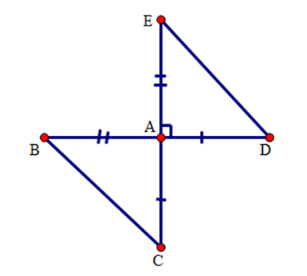
Xét hai tam giác $AED$ và tam giác $ABC$ có:
$AE = AB;$\(\widehat {EAD} = \widehat {BAC}\)(hai góc đối đỉnh); $AD = AC,$
do đó \(\Delta AED = \Delta ABC\) (c.g.c) (A đúng).
Suy ra $BC = ED$ (hai cạnh tương ứng) (B đúng); \(\widehat {ABC} = \widehat {AED}\) (hai góc tương ứng) (D đúng).
Cho tam giác $BAC$ và tam giác $KEF$ có $BA = EK,$ \(\widehat A = \widehat K\), $CA = KF.$ Phát biểu nào trong trong các phát biểu sau đây là đúng :
-
A.
\(\Delta BAC = \Delta EKF\)
-
B.
\(\Delta BAC = \Delta EFK\)
-
C.
\(\Delta {\rm A}BC = \Delta FKE\)
-
D.
\(\Delta BAC = \Delta KEF\)
Đáp án : A
Xét tam giác $BAC$ và tam giác $KEF$ có $BA = EK,$ \(\widehat A = \widehat K\), $CA = KF.$ Suy ra \(\Delta BAC = \Delta EKF\) (c.g.c)
Cho tam giác $ABC$ và tam giác $MHK$ có: $AB = MH$ , \(\widehat A = \widehat M\). Cần thêm một điều kiện gì để hai tam giác $ABC$ và $MHK$ bằng nhau theo trường hợp cạnh – góc – cạnh:
-
A.
$BC = MK$
-
B.
$BC = HK$
-
C.
$AC = MK$
-
D.
$AC = HK$
Đáp án : C
Để tam giác $ABC$ và tam giác $MHK$ bằng nhau theo trường hợp cạnh – góc – cạnh cần thêm điều kiện về cạnh kề đó là:$AC = MK.$