Tổng hợp 20 đề thi học kì 1 Toán 9 có đáp án
Tổng hợp 20 đề thi học kì 1 Toán 9 có đáp án
Đề 1
Bài 1: (2 điểm)
1) Thực hiện phép tính:
a) \(\sqrt 8 - 2\sqrt {18} + 5\sqrt {32} - \sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} \)
b) \(\dfrac{{5 + 6\sqrt 5 }}{{\sqrt 5 }} + \dfrac{{7 - \sqrt 7 }}{{\sqrt 7 - 1}} - \left( {\sqrt 5 + \sqrt 7 } \right)\)
2) Giải phương trình: \(x - \sqrt {x - 15} = 17\).
Bài 2: (2,5 điểm) Cho biểu thức \(P = \dfrac{{3x + \sqrt {9x} - 3}}{{x + \sqrt x - 2}} - \dfrac{{\sqrt x + 1}}{{\sqrt x + 2}} + \dfrac{{\sqrt x - 2}}{{1 - \sqrt x }}\) với \(x \ge 0,x \ne 1\)
a) Rút gọn biểu thức \(P\).
b) So sánh \(P\) với \(\sqrt P \) với điều kiện \(\sqrt P \)có nghĩa
c) Tìm \(x\) để \(\dfrac{1}{P}\) nguyên.
Câu 3: (2 điểm) (VD) Cho đường thẳng \(\left( {{d_1}} \right) :y = \left( {m - 1} \right)x + 2m + 1\).
a) Tìm \(m\) để đường thẳng \({d_1}\) cắt trục tung tại điểm có tung độ là \( - 3\). Vẽ đồ thị hàm số vừa tìm được và chứng tỏ giao điểm của đồ thị hàm số vừa tìm được với đường thẳng \(\left( d \right):y = x + 1\) nằm trên trục hoành.
b) Tìm \(m\) để khoảng cách từ gốc tọa độ đến đường thẳng \({d_1}\) đạt giá trị lớn nhất.
Bài 4: (3 điểm) Cho điểm M bất kì trên đường tròn tâm O đường kính AB . Tiếp tuyến tại M và tại B của \(\left( O \right)\) cắt nhau tại D. Qua O kẻ đường thẳng vuông góc với OD cắt MD tại C và cắt BD tại N.
a) Chứng minh \(DC = DN\).
b) Chứng minh AC là tiếp tuyến của đường tròn tâm O .
c) Gọi H là chân đường vuông góc kẻ từ M xuống AB, I là trung điểm MH. Chứng minh B, C, I thẳng hàng.
d) Qua O kẻ đường vuông góc với AB , cắt \(\left( O \right)\) tại K ( K và M nằm khác phía với đường thẳng AB ). Tìm vị trí của M để diện tích tam giác MHK lớn nhất.
Bài 5: (0,5 điểm)
Cho các số thực dương \(x,y,z\) thỏa mãn \(x + 2y + 3z \ge 20\). Tìm giá trị nhỏ nhất của biểu thức : \(A = x + y + z + \dfrac{3}{x} + \dfrac{9}{{2y}} + \dfrac{4}{z}\).
Đề 2
Bài 1: (3 điểm) . Thực hiện các phép tính
a) \(2\sqrt {75} - 3\sqrt {27} - \dfrac{1}{4}\sqrt {192} \).
b) \(\sqrt {4 + 2\sqrt 3 } + \sqrt {{{\left( {\sqrt 3 - 2} \right)}^2}} \).
c) \(\dfrac{{\sqrt {15} - \sqrt {12} }}{{\sqrt 5 - 2}} - \dfrac{1}{{2 - \sqrt 3 }}\).
d) \(\left( {\dfrac{{\sqrt x - 2}}{{\sqrt x + 2}} - \dfrac{{\sqrt x + 2}}{{\sqrt x - 2}}} \right).\left( {\sqrt x - \dfrac{4}{{\sqrt x }}} \right)\left( {x > 0;x \ne 4} \right)\).
Bài 2: (2 điểm) Cho hai hàm số bậc nhất \(y = - \dfrac{1}{2}x\) có đồ thị là \(\left( {{d_1}} \right)\) và \(y = 2x - 5\) có đồ thị là \(\left( {{d_2}} \right)\)
a) Vẽ \(\left( {{d_1}} \right),\left( {{d_2}} \right)\) trên cùng hệ trục tọa độ.
b) Cho đường thẳng \(\left( {{d_3}} \right):y = ax + b.\) Tìm \(a,b\) để \({d_3}//{d_1}\) và cắt \(\left( {{d_2}} \right)\) tại một điểm có tung độ bằng 3.
Bài 3: (1 điểm). Tìm \(x\) biết \(\sqrt {4x - 20} = 7\sqrt {\dfrac{{x - 5}}{9}} - 2\).
Bài 4: (0,5 điểm) Năm nay số dân ở một thành phố A có 2 000 000 người. Hỏi 2 năm sau số dân của thành phố A là bao nhiêu người? Biết rằng bình quân mỗi năm số dân của thành phố A này tăng 0,5%.
Bài 5: (0,5 điểm) Các tia sáng mặt trời tạo với mặt đất một góc xấp xỉ \({30^o}\). Tại thời điểm đó, bóng của một cái cây trên mặt đất dài \(20m\). Hỏi cái cây đó cao bao nhiêu mét ? (làm tròn tới phần thập phân thứ nhất).
Bài 6: (3 điểm) Từ điểm \(M\) nằm ở ngoài đường tròn \(\left( {O,R} \right)\) với \(OM > 2R\), vẽ hai tiếp tuyến \(MA,MB\;\;(A,B\)là hai tiếp điểm). Gọi \(H\)là giao điểm của \(AB,OM\)
a)Nếu cho \(OM = R\sqrt 5 \). Tính độ dài đoạn \(MA\) theo \(R\) và số đo \(\angle AOM\) (làm tròn tới độ).
b)Chứng minh bốn điểm \(M,A,O,B\) thuộc một đường tròn.
c)Gọi \(AC\) là đường kính của đường tròn\(\left( O \right)\), tia \(CH\) cắt đường tròn \(\left( O \right)\)tại \(N\). Chứng minh \(4OH.OM = A{C^2}\).
d) Chứng minh rằng đường thẳng \(AN\) đi qua trung điểm của \(MH\)
Đề 3
Bài 1: (1,5 điểm) Tính:
a)\(4\sqrt {12} - 15\sqrt {\dfrac{1}{3}} - \dfrac{{9 - \sqrt 3 }}{{\sqrt 3 }}\)
b)\(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} - \sqrt {\dfrac{8}{{7 - 3\sqrt 5 }}} \).
Bài 2: (1,5 điểm)
a)Giải phương trình sau: \(\sqrt {36{x^2} - 12x + 1} = 2\).
b) Rút gọn: \(A = \dfrac{x}{{\sqrt x - 1}} - \dfrac{{2x - \sqrt x }}{{x - \sqrt x }}\) ( với \(x > 0,x \ne 1\)).
Bài 3: (2 điểm)
a)Một khu vườn hình chữ nhật có kích thước là 25m và 40m. Người ta tăng mỗi kích thước của khu vườn thêm \(x\) (m). Gọi \(S,P\) theo thứ tự là diện tích và chu vi của khu vườn mới tính theo \(x\). Hỏi các đại lương \(S,P\) có phải là hàm số bậc nhất của \(x\) không? Vì sao? Tính giá trị của \(x\) khi biết giá trị tương ứng của \(P\) là 144 (tính theo đơn vị m).
b) Cho hàm số \(y = - 2x + 3\) có đồ thị \(\left( {{d_1}} \right)\)và hàm số \(y = x\) có đồ thị là \(\left( {{d_2}} \right)\). Vẽ \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) trên cùng mặt phẳng tọa độ. Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) bằng phép tính.
Bài 4: (2 điểm)
a) Muốn tính khoảng cách từ điểm A đến điểm B bên kia bờ sông, ông Việt vạch từ A đường vuông góc với AB . Trên đường vuông góc này lấy một đoạn thẳng \(AC = 30m\), rồi vạch \(CD\) vuông góc với phương BC cắt AB tại D . Do\(AD = 20m\), từ đó ông Việt tính được khoảng cách từ A đến B . Em hãy tính độ dài AB và số đo góc \(\angle ACB\).
b) Có 150g dung dịch chứa 40g muối. Ta phải pha thêm bao nhiêu nước nữa để dung dịch có tỉ lên 20% muối
Bài 5: (3 điểm) Cho điểm A nằm ngoài đường tròn \(\left( {O;R} \right)\), vẽ hai tiếp tuyến AB, AC với đường tròn \(\left( {O;R} \right)\) ( B, C là tiếp điểm), gọi H là giao điểm của OA và BC.
a) Chứng minh rằng: \(OA \bot BC\).
b) Gọi D, E là giao điểm của OA với đường tròn \(\left( {O;R} \right)\) ( D nằm giữa O và A). Chứng minh rằng \(OH.HA = HD.HE\).
c)Chứng minh rằng \(2HD.AB = DA.BC\).
Đề 4
Bài 1: (2 điểm) Thực hiện phép tính:
a) \(A = 3\sqrt {32} - 6\sqrt 2 - \sqrt {50} \)
b) \(B = \sqrt {{{\left( {5 + \sqrt 3 } \right)}^2}} + \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} \)
Bài 2: (2 điểm)
Cho đường thẳng \(\left( {{d_1}} \right):y = 2x - 1\) và đường thẳng \(\left( {{d_2}} \right):y = x + 1\)
a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm \(B\) của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) bằng phép toán.
Bài 3: (1 điểm) Rút gọn biểu thức sau
a) \(C = \dfrac{{\sqrt {14} + \sqrt 7 }}{{\sqrt 2 + 1}} - \sqrt 7 \)
b) \(D = \left( {4 - \sqrt {15} } \right){\left( {\sqrt {2 - \sqrt 3 } + \sqrt {3 + \sqrt 5 } } \right)^2}\)
Bài 4: (1 điểm)
Nhân ngày “Black Friday” (24/11/2017). Một cửa hàng điện tử thực hiện giảm giá 50% trên một tivi trong lô hàng gồm 40 cái tivi với giả bán lẻ ban đầu là 6.500.000 đ/cái. Đến trưa cùng ngày đã bán được 20 cái, khi đó cửa hàng quyết định giảm thêm 10% nữa trên giá đang bán cho mỗi tivi thì bán được hết lô hàng. Biết rằng giá vốn là 3.050.000 đ/một tivi. Hỏi cửa hàng đó lời hay lỗ khi bán hết lô hàng tivi?
Bài 5: (1 điểm)
Tính chiều cao của một ngọn núi (làm tròn đến mét), biết tại hai điểm A, B cách nhau 500m , người ta nhìn thấy đỉnh núi với góc nắng lần lượt là \({34^o}\) và \({38^o}\).
Bài 6: (1 điểm)
Hiện nay tại nước Mỹ quy định cầu thang cho người khuyết tật dùng xe lăn có hệ số góc không quá \(\dfrac{1}{{12}}\). Để phù hợp với tiêu chuẩn ấy thì chiều cao cầu thang tối đa là bao nhiêu khi biết đáy của cầu thang có độ dài là 4m ?
Bài 7: (2 điểm)
Cho nửa đường tròn \(\left( O \right)\)đường kính \(AB\). Vẽ các tiếp tuyến \(Ax,By\). Từ một điểm M trên nửa đường tròn vẽ tiếp tuyến với \(\left( O \right)\) cắt \(Ax,By\) lần lượt tại D , C .
a) Chứng minh: \(CD = AD + BC\) và \(\angle COD = {90^o}\).
b) Gọi N là giao điểm của AC và BD . Chứng minh MN vuông góc với AB .
Đề 5
Câu 1: (2 điểm)
Thực hiện phép tính:
a) \(3\sqrt {80} - 2\sqrt {45} - \sqrt {125} \).
b) \(\dfrac{3}{{\sqrt 7 - 1}} - \dfrac{{\sqrt 7 - \sqrt {21} }}{{2 - 2\sqrt 3 }}\).
c) \(\sqrt {{{\left( {2\sqrt 5 - 5} \right)}^2}} + \sqrt {24 - 8\sqrt 5 } \).
Câu 2: (1 điểm)
Giải phương trình:
a)\(\sqrt {4 - 3x} = 4\).
b)\(\sqrt {4{x^2} + 4x + 1} = 5\).
Câu 3: (1,5 điểm)
Cho hàm số \(y = - \dfrac{1}{2}x\) có đồ thị \(\left( {{d_1}} \right)\) và hàm số \(y = x - 3\) có đồ thị \(\left( {{d_2}} \right)\).
a)Vẽ \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) trên cùng hệ trục tọa độ
b)Tìm tọa độ giao điểm A của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) bằng phép toán.
Câu 4: (1 điểm)
Một máy bay cất cánh theo phương có góc nâng là \({23^o}\)so với mặt đất. Hỏi muốn đạt độ cao 250m so với mặt đất thì máy bay phải bay lên một đoạn đường là bao nhiêu mét? (làm tròn đến mét)
Câu 5: (1 điểm)
Một hỗn hợp dung dịch gồm nước và muối trong đó 6% muối (về khối lượng). Hỏi phải thêm bao nhiêu kg nước vào 50kg dung dịch trên để có được một dung dịch mới có 3% muối.
Câu 6: (1 điểm)
Một cửa hàng có hai loại quạt, giá tiền như nhau. Quạt màu xanh được giảm giá hai lần, mỗi lần giảm giá 10% so với giá đang bán. Quạt màu đỏ được giảm giá một lần 20%. Hỏi sau khi giảm giá như trên thì loại quạt nào rẻ hơn.
Câu 7: (2,5 điểm)
Cho \(\left( O \right)\)đường kính \(AB\). Lấy C thuộc \(\left( O \right)\), gọi E là trung điểm BC . Tiếp tuyến tại C của \(\left( O \right)\)cắt OE ở D
a)Chứng minh: \(\Delta ACB\)vuông và \(OE \bot BC\).
b)Chứng minh: DB là tiếp tuyến của \(\left( O \right)\).
c)Kẻ CH vuông góc với AB . Chứng minh: \(CB.OC = OD.HC\).
Đề 6
Bài 1: (2 điểm) Thực hiện phép tính (thu gọn):
1) \(2\sqrt {48} + \dfrac{1}{3}\sqrt {108} - 5\sqrt 3 - 3\sqrt {27} \).
2) \(\dfrac{{6 - \sqrt 6 }}{{\sqrt 6 - 1}} - 9\sqrt {\dfrac{2}{3}} - \dfrac{4}{{2 - \sqrt 6 }}\).
Bài 2: (1 điểm) Giải phương trình: \(\dfrac{5}{3}\sqrt {9x - 18} - \dfrac{1}{2}\sqrt {16x - 32} - 15 = 0\).
Bài 3: (1,75 điểm) Cho hàm số \(y = 3x\) có đồ thị \(\left( D \right)\) và hàm số \(y = x + 2\) có đồ thị \(\left( {{D_1}} \right)\).
1) Vẽ \(\left( D \right)\)và \(\left( {{D_1}} \right)\) trên cùng một mặt phẳng tọa độ \(Oxy\).
2) Tìm \(m\) để đường thẳng \(y = \left( {m - 5} \right)x + m + 2\) có đồ thị \(\left( {{D_2}} \right)\) cắt \(\left( {{D_1}} \right)\)tại điểm B có hoành độ bằng 2.
Bài 4: (3,25 điểm) Cho tam giác ABC vuông tại A , đường tròn \(\left( O \right)\)đường kính AC cắt BC tại K , vẽ dây cung AD của \(\left( O \right)\) vuông góc với BO tại H .
1) Chứng minh bốn điểm B , K , H , A cùng thuộc một đường tròn.
2) Chứng minh: BD là tiếp tuyến của đường tròn \(\left( O \right)\)
3) Chứng minh \(BH.BO = BK.BC\).
4) Từ \(\left( O \right)\)vẽ đường thẳng song song với AD cắt tia BA tại E , từ B vẽ đường thẳng vuông góc với EC tại F , BF cắt AO tại M . Chứng minh: \(MA = MO\)
Bài 5: (1 điểm) Nhà bạn Bình có gác lửng cao so với nền nhà là 3m. Ba bạn Bình cần đặt một thang đi lên gác, biết khi đặt thang phải để thang tạo được với mặt đất một góc \({70^o}\)thì đảm bảo sự an toàn khi sử dụng. Với kiến thức đã học, Bình hãy giúp Ba tính chiều dài thang là bao nhiêu mét để sử dụng. (kết quả làm tròn đến chữ số thập phân thứ nhất)
Bài 6: (1 điểm)
Tháng 11 vừa qua có ngày Black Friday, phần lớn các trung tâm thương mại đều giảm giá rất nhiều mặt hàng. Mẹ bạn An có dẫn An đến một trung tâm thương mại để mua một đôi giày. Biết đôi giày đang khuyến mại giảm giá 40%, mẹ bạn An có thẻ khách hàng thân thiết của trung tâm thương mại nên được giảm thêm 5% trên giá đã giảm nữa, do đó mẹ bạn An phải trả 684.000 đ cho đôi giày. Hỏi giá ban đầu của đôi giày nếu không khuyến mại là bao nhiêu?
Đề 7
Bài 1: (2 điểm)
a) Tính chu vi tam giác ABC biết độ dài 3 cạnh là \(AB = 5\sqrt 2 \left( {cm} \right),AC = \sqrt {32} \left( {cm} \right)\),\(BC = \sqrt {98} \left( {cm} \right)\). (Không yêu cầu vẽ hình)
b) Thu gọn: \(B = \sqrt {{{\left( {\sqrt 7 - 1} \right)}^2}} - \dfrac{6}{{\sqrt 7 - 1}}\).
Bài 2: (3,0 điểm) Cho đường thẳng \(\left( {{d_1}} \right):y = - 3x + 1\) và đường thẳng \(\left( {{d_2}} \right):y = x - 3\).
a)Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng mặt phẳng tọa độ \(Oxy\).
b)Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) bằng phép tính.
c)Tìm \(m\) để đường thẳng \(\left( D \right):y = \left( {2m + 3} \right)x - 5\) song song vơi đường thẳng \(\left( {{d_1}} \right)\).
Bài 3: (1 điểm) Trong một tòa nhà ngoài thang máy người ta còn xây thêm một cầu thang đi bộ. Từ tầng 1 đến tầng 2 có 30 bậc thang. Các tầng còn lại cứ hai tầng liên tiếp cách nhau 21 bậc thang. Do thang máy bị hư nên bạn Vy đi bộ bắt đầu từ tầng 1 về căn hộ của mình. Tổng số bậc thang Vy đã đi là 135. Hỏi căn hộ của Vy ở tầng thứ bao nhiêu của tòa nhà?
Bài 4: (1 điểm) Tàu ngầm đang ở trên mặt biển bỗng đột ngột lặn xuống theo phương tạo với mặt nước biển một góc\({21^o}\). Nếu tàu chuyển động theo phương lặn xuống được 300m thì nó ở độ sâu bao nhiêu? Khi đó khoảng cách theo phương nằm ngang so với nơi xuất phát là bao nhiêu mét ? (kết quả làm tròn đến mét)
Bài 5: (3,0 điểm) Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính AB . Vẽ các tiếp tuyến \(Ax\) và \(By\) của đường tròn \(\left( {O;R} \right)\).
a)Chứng minh: \(Ax//By\).
b)Trên \(\left( {O;R} \right)\)lấy điểm M . Tiếp tuyến tại M của đường tròn \(\left( {O;R} \right)\)lần lượt cắt \(Ax\) và \(By\) tại D và E . Chứng minh: \(DE = DA + BE\).
c)Chứng minh: \(\angle DOE = {90^o}\) và \(DA.BE = {R^2}\).
Đề 8
Bài 1: (1 điểm) Thực hiện phép tính:
1) \(A = \sqrt {12} - 2\sqrt {48} + \dfrac{7}{5}\sqrt {75} \)
2) \(B = \sqrt {14 - 6\sqrt 5 } + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} \)
Bài 2: (2,5 điểm)
1)Cho biểu thức \(A = \dfrac{{\sqrt x + 4}}{{\sqrt x + 2}}\left( {x \ge 0} \right)\). Tính giá trị biểu thức \(A\) khi \(x = 36\).
2)Rút gọn biểu thức \(B = \left( {\dfrac{{\sqrt x }}{{\sqrt x + 4}} + \dfrac{4}{{\sqrt x - 4}}} \right):\dfrac{{x + 16}}{{\sqrt x + 2}}\) (với \(x \ge 0,x \ne 16\)).
3)Với các biểu thức \(A,B\)nói trên, hãy tìm các giá trị nguyên của \(x\) để giá trị của biểu thức \(P = B\left( {A - 1} \right)\)là số nguyên.
Bài 3: (1,5 điểm) Cho hàm số \(y = 2x + 4\) có đồ thị là \(\left( {{d_1}} \right)\)và hàm số \(y = - x + 1\) có đồ thị là \(\left( {{d_2}} \right)\)
1)Vẽ \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ .
2)Gọi A là giao điểm của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\). Tìm tọa độ của điểm A .
3)Xác định các hệ số \(a,b\) của đường thẳng \({d_3}:y = ax + b\). Biết rằng \(\left( {{d_3}} \right)\)song song với \(\left( {{d_1}} \right)\) và \(\left( {{d_3}} \right)\)cắt \(\left( {{d_2}} \right)\) tại một điểm có hoành độ bằng 2.
Bài 4: (4,5 điểm)
1)Cho tam giác ABC vuông tại A có AH là đường cao. Biết \(BH = 9\)cm, \(HC = 16\)cm. Tính độ dài AH, AC , số đo \(\angle ABC\) (số đo làm tròn đến độ).
2)Cho nửa đường tròn tâm O đường kính AB . Trên nửa mặt phẳng bờ AB chứa nửa đường tròn, kẻ hai tiếp tuyến Ax, By với nửa đường tròn, M là một điểm nằm trên nửa đường tròn ( M khác A và B ), từ M kẻ tiếp tuyến với nửa đường tròn cắt Ax, By lần lượt tại C và D.
a)Chứng minh rằng: \(CD = AC + BD\)
b) AM cắt OC tại E, BM cắt OD tại F. Chứng minh \(EF = OM\).
c)Chứng minh rằng tích \(AC.BD\) không phụ thuộc vào vị trí của điểm M.
d)Kẻ MH vuông góc với AB tại H, MH cắt BC tại I. Chứng minh rằng I là trung điểm của MH.
Bài 5: (0,5 điểm)
Cho \(a,b,c\)là các số dương thỏa mãn điều kiện \(a + b + c + ab + bc + ca = 6\). Chứng minh rằng: \(\dfrac{{{a^3}}}{b} + \dfrac{{{b^3}}}{c} + \dfrac{{{c^3}}}{a} \ge {a^2} + {b^2} + {c^2} \ge 3\)
Đề 9
Phần I: Trắc nghiệm (2 điểm)
Hãy chọn chữ cái đứng trước câu trả lời đúng cho các câu hỏi sau:
Câu 1 : Điều kiện để biểu thức\(A = \dfrac{{2017}}{{\sqrt x - 1}}\) xác định là:
A. \(x > 0\)
B.\(x > 1\)
C. \(x > 0,x \ne 1\)
D.\(x \ge 0,x \ne 1\)
Câu 2 (TH): Cho\(\sqrt {x - 1} = 2\), giá trị của \(x\) là:
A. \( - 3\) B. 3
C. \( - 1\) D. 5
Câu 3 : Cho biểu thức \(P = \sqrt {\dfrac{{5a}}{{32}}} .\sqrt {\dfrac{{2a}}{5}} \) với \(a \ge 0\), kết quả thu gọn của \(P\) là:
A.\(\dfrac{{\sqrt a }}{{16}}\) . B.\(\dfrac{a}{4}\) .
C. \(\dfrac{a}{{16}}\). D.\(\dfrac{{\sqrt a }}{4}\) .
Câu 4 : Trong các hàm số dưới đây, hàm số bậc nhất có đồ thị đi qua điểm \(A\left( {1;4} \right)\)là:
A. \(y = {x^2} + 3\) B.\(y = x - 3\)
C. \(y = 4x\). D.\(y = 4 - x\) .
Câu 5 : Cho 2 đường thẳng \(\left( {{d_1}} \right):y = \left( {{m^2} + 1} \right)x + 2\) và \(\left( {{d_2}} \right):y = 5x + m\). Hai đường thẳng đó trùng nhau khi:
A. \(m = \pm 2\) B.\(m = 2\)
C. \(m = - 2\) D.\(m \ne \pm 2\)
Câu 6 : Cho tam giác ABC vuông tại A . Trong các hệ thức sau, hệ thức đúng là:
A.\(\sin C = \dfrac{{BC}}{{AC}}\)
B.\(\cos C = \dfrac{{BC}}{{AC}}\)
C. \(\tan C = \dfrac{{AB}}{{AC}}\)
D. \(\cot C = \dfrac{{AB}}{{AC}}\)
Câu 7 : Cho hai điểm phân biệt A, B . Số đường thẳng đi qua hai điểm A, B là:
A. 0 B. 1
C. 2 D. Vô số
|
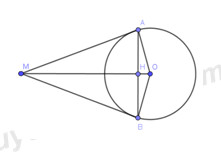
Câu 8 : Cho hình vẽ, MA và MB là hai tiếp tuyến của đường tròn \(\left( {O,3cm} \right)\), \(MA = 4cm\). Độ dài đoạn thẳng AB là: A. 4,8cm B. 2,4cm C. 1,2cm D. 9,6cm |
|
Phần II. Tự luận (8 điểm)
Câu 1: (2 điểm)
Cho hai biểu thức \(A = \dfrac{{\sqrt x - 5}}{{\sqrt x }}\) và \(B = \dfrac{{\sqrt x }}{{\sqrt x - 5}} - \dfrac{{3\sqrt x }}{{x - 25}}\) với\(x > 0,x \ne 25\).
a) Tính giá trị biểu thức \(A\) khi\(x = 81\).
b) Cho\(P = A.B\), chứng minh rằng \(P = \dfrac{{\sqrt x + 2}}{{\sqrt x + 5}}\)
c) So sánh \(P\) và\({P^2}\).
Câu 2: (2 điểm)
Cho hàm số \(y = \left( {m + 2} \right)x + 2{m^2} + 1\) (\(m\)là tham số)
a)Vẽ đồ thị hàm số trên khi\(m = - 1\).
b)Tìm \(m\)để hai đường thẳng \(\left( d \right)y = \left( {m + 2} \right)x + 2{m^2} + 1\)và \(\left( {d'} \right):y = 3x + 3\) cắt nhau tại một điểm trên trục tung.
Câu 3: (3,5 điểm)
Cho đường tròn \(\left( O \right)\) đường kính AB và điểm C thuộc đường tròn \(\left( O \right)\)( C khác A và B ) sao cho\(AC > BC\). Qua O vẽ đường thẳng vuông góc với dây cung AC tại H . Tiếp tuyến tại A của đường tròn \(\left( O \right)\) cắt OH tại D . Đoạn thẳng DB cắt đường tròn \(\left( O \right)\) tại E .
a) Chứng minh \(HA = HC,\angle DCO = {90^o}\)
b) Chứng minh rằng \(DH.DO = DE.DB\)
c) Trên tia đối của tia EA lấy điểm F sao cho E là trung điểm cạnh AF . Từ F vẽ đường thẳng vuông góc với đường thẳng AD tại K . Đoạn thẳng FK cắt đường thẳng BC tại M . Chứng minh\(MK = MF\).
Câu 4: (0,5 điểm)
Cho các số dương \(x,y\) thoả mãn\(x + y \le \dfrac{4}{3}\). Tìm giá trị nhỏ nhất của biểu thức
\(S = x + y + \dfrac{3}{{4x}} + \dfrac{3}{{4y}}\)
Đề 10
Câu 1 (2,0 điểm): Hãy tính giá trị của:
a) \(M = \left( {2\sqrt {300} + 3\sqrt {48} - 4\sqrt {75} } \right):\sqrt 3 \) ;
b) \(N = \sqrt {{{\left( {\sqrt 3 - 2} \right)}^2}} + \sqrt {4 - 2\sqrt 3 } \) ;
c) \(P = \dfrac{2}{{\sqrt 3 + 1}} - \dfrac{1}{{\sqrt 3 - 2}} + \dfrac{{12}}{{\sqrt 3 + 3}}\) ;
Câu 2 (2,0 điểm): Cho các biểu thức:
\(A = 1 - \dfrac{{\sqrt x }}{{1 + \sqrt x }}\) và \(B = \dfrac{{\sqrt x + 3}}{{\sqrt x - 2}} + \dfrac{{\sqrt x + 2}}{{3 - \sqrt x }} + \dfrac{{\sqrt x + 2}}{{x - 5\sqrt x + 6}}\) với \(x \ge 0,\,\,x \ne 4,\,\,x \ne 9.\)
a) Hãy tính giá trị của A khi \(x = 16\).
b) Rút gọn B .
c) Xét biểu thức \(T = \dfrac{A}{B}\) . Hãy tìm giá trị nhỏ nhất của T .
Câu 3 (2,0 điểm): Cho hàm số \(y = \left( {2 - m} \right)x + m + 1\) (với m là tham số và \(m \ne 2\)) có đồ thị là đường thẳng \(\left( d \right).\)
a) Khi \(m = 0\), hãy vẽ \(\left( d \right)\) trên hệ trục tọa độ \(Oxy\).
b) Tìm m để \(\left( d \right)\) cắt đường thẳng \(y = 2x - 5\) tại điểm có hoành độ bằng 2.
c) Tìm m để \(\left( d \right)\) cùng với các trục tọa độ \(Ox,\,\,Oy\) tạo thành một tam giác có diện tích bằng 2.
Câu 4 (3,5 điểm): Cho đường tròn \(\left( {O;R} \right)\) và điểm A nằm ngoài \(\left( O \right)\). Từ A kẻ hai tiếp tuyến AB, AC với \(\left( O \right)\) ( B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC .
a) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn.
b) Chứng minh OA là đường trung trực của BC .
c) Lấy D đối xứng với B qua O . Gọi E là giao điểm của đoạn thẳng AD với \(\left( O \right)\) ( E không trùng với D ). Chứng minh \(\dfrac{{DE}}{{BE}} = \dfrac{{BD}}{{BA}}\).
d) Tính số đo góc HEC .
Câu 5 (0,5 điểm): Cho \(x > 0,\,\,y > 0\) thỏa mãn \(xy = 6\). Tìm giá trị nhỏ nhất của biểu thức:
\(Q = \dfrac{2}{x} + \dfrac{3}{y} + \dfrac{6}{{3x + 2y}}\) .
Đề 11
Câu 1 (2,5 điểm): Cho hai biểu thức\(A = \frac{{x - 2\sqrt x + 9}}{{\sqrt x - 3}}\)và \(B = \frac{{\sqrt x + 3}}{{\sqrt x - 3}} + \frac{{\sqrt x }}{{\sqrt x + 3}} - \frac{{x + 9}}{{x - 9}}\)với \(x > 0,\,\,x \ne 9\)
1) Tính giá trị của biểu thức A khi \(x = 3\)
2) Chứng minh \(B = \frac{{\sqrt x }}{{\sqrt x - 3}}\)
3) So sánh \(\frac{A}{B}\) và 4.
Câu 2 (2,5 điểm): Cho hàm số \(y = \left( {m + 1} \right)x + m\) (với \(m \ne - 1\)có đồ thị là đường thẳng \(\left( d \right)\)
1) Tìm giá trị của m để đường thẳng \(\left( d \right)\) cắt trục tung tại điểm có tung độ là 1
2) Trên mặt phẳng tọa độ Oxy , vẽ đường thẳng \(\left( d \right)\) với giá trị m tìm được ở câu 1
3) Tìm giá trị của m để đường thẳng \(\left( d \right)\) cắt đường thẳng \(y = 3x + 2\) tại một điểm nằm trên trục hoành
Câu 3 (1,0 điểm):
Giải hệ phương trình: \(\left\{ \begin{array}{l}x + \left( {\sqrt 2 - 1} \right)y = 1\\\left( {\sqrt 2 + 1} \right)x - y = \sqrt 2 + 1\end{array} \right.\)
Câu 4 (3,5 điểm): Cho đường tròn \(\left( {O;R} \right)\) và một điểm H cố định nằm ngoài đường tròn. Qua H kẻ đường thẳng d vuông góc với đoạn thẳng OH . Từ một điểm S bất kì trên đường thẳng d kẻ hai tiếp tuyến SA, SB với đường tròn \(\left( {O;R} \right)\) ( A, B là tiếp điểm). Gọi M,N lần lượt là giao điểm của đoạn thẳng SO với đoạn thẳng AB và với đường tròn \(\left( {O;R} \right)\).
1) Chứng minh bốn điếm S, A, O, B cùng nằm trên một đường tròn
2) Chứng minh \(OM.OS = {R^2}\)
3) Chứng minh N là tâm đường tròn nội tiếp tam giác SAB
4) Khi điểm S di chuyển trên đường thẳng d thì điểm M di chuyển trên đường nào? Tại sao?
Câu 5 (0,5 điểm): Cho ba số thực dương \(x,\,y,\,z\) thỏa mãn \(x + y + z = 1\)
Chứng minh rằng \(P = \frac{{5{y^3} - {x^3}}}{{yx + 3{y^2}}} + \frac{{5{z^3} - {y^3}}}{{zy + 3{z^2}}} + \frac{{5{x^3} - {z^3}}}{{xz + 3{x^2}}} \le 1\)
Đề 12
I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Chọn chữ cái đứng trước câu trả lời đúng và ghi vào tờ giấy thi của em.
Câu 1 : Căn bậc hai số học của \(16\) là
A. \(4\) B.\( - 4\)
C. \( \pm 4\) D.\(256\)
Câu 2 : Điều kiện xác định của biểu thức \(\sqrt {\dfrac{{2017}}{{x - 2018}}} \) là
A. \(x \ge 2018\) B.\(x \ne 2018\)
C. \(x > 2018\) D.\(x < 2018\)
Câu 3 : Rút gọn biểu thức \(\sqrt {7 - 4\sqrt 3 } + \sqrt 3 \) ta được kết quả là
A. \(2\) B.\(2\sqrt 3 - 2\)
C. \(2\sqrt 3 + 2\) D.\(2 - \sqrt 3 \)
Câu 4 : Hàm số \(y = (m - 2017)x + 2018\) đồng biến khi
A. \(m \ne 2017\) B.\(m \ge 2017\)
C. \(m > 2017\) D.\(m < 2017\)
Câu 5 : Tìm giá trị của \(m\) để đồ thị của hàm số \(y = (m - 2017)x + 2018\) đi qua điểm \((1\,;\,\,1)\) ta được
A. \(m = 2017\) B.\(m = 0\)
C. \(m > 2017\) D.\(m < 2017\)
Câu 6 : Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 3,AB = 4\). Khi đó \(\cos B\) bằng
A. \(\dfrac{3}{4}\) B.\(\dfrac{3}{5}\)
C. \(\dfrac{4}{3}\) D.\(\dfrac{4}{5}\)
Câu 7 : Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(AB = 9cm,\,\,BC = 15cm\). Khi đó độ dài \(AH\) bằng:
A. \(6,5cm\) B.\(7,2cm\)
C. \(7,5cm\) D.\(7,7cm\)
Câu 8 : Giá trị của biểu thức \(P = {\cos ^2}{20^0} + {\cos ^2}{40^0} + {\cos ^2}{50^0} + {\cos ^2}{70^0}\) bằng
A. \(0\) B.\(1\)
C. \(2\) D.\(3\)
II. TỰ LUẬN (8,0 điểm):
Bài 1 (1,75 điểm):
Cho biểu thức \(P = \dfrac{{\sqrt x }}{{\sqrt x + 3}} + \dfrac{{2\sqrt x }}{{\sqrt x - 3}} - \dfrac{{3x + 9}}{{x - 9}}\) với \(x \ge 0,\,\,x \ne 9\).
a) Rút gọn biểu thức \(P\).
b) Tính giá trị của biểu thức \(P\) tại \(x = 4 - 2\sqrt 3 \).
Bài 2 (2,0 điểm):
Cho hàm số \(y = (m - 1)x + m\).
a) Xác định giá trị của \(m\) để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng \(2\).
b) Xác định giá trị của \(m\) để đồ thị của hàm số cắt hoành tại điểm có hoành độ bằng \( - 3\).
c) Vẽ đồ thị của hai hàm số ứng với giá trị của \(m\) tìm được ở các câu a) và b) trên cùng hệ trục tọa độ \(Oxy\) và tìm tọa độ giao điểm của hai đường thẳng vừa vẽ được.
Câu 3 (3,0 điểm):
Cho đường tròn \((O,R)\,\)và đường thẳng \(d\) cố định không cắt đường tròn. Từ một điểm \(A\) bất kì trên đường thẳng \(d\) kẻ tiếp tuyến \(AB\) với đường tròn (\(B\) là tiếp điểm). Từ \(B\) kẻ đường thẳng vuông góc với \(AO\) tại \(H\), trên tia đối của tia \(HB\) lấy điểm \(C\) sao cho \(HC = HB\).
a) Chứng minh \(C\) thuộc đường tròn \((O,R)\,\)và \(AC\) là tiếp tuyến của đường tròn \((O,R)\,\).
b) Từ \(O\) kẻ đường thẳng vuông góc với đường thẳng \(d\) tại \(I\), \(OI\) cắt \(BC\) tại \(K\). Chứng minh \(OH.OA = OI.OK = {R^2}\).
c) Chứng minh khi \(A\) thay đổi trên đường thẳng \(d\) thì đường thẳng \(BC\) luôn đi qua một điểm cố định.
Câu 4 (1,25 điểm):
a) Tìm giá trị nhỏ nhất của biểu thức \(Q = x - 2\sqrt {2x - 1} \).
b) Giải phương trình \(\sqrt {{x^2} - 3x + 2} + 3 = 3\sqrt {x - 1} + \sqrt {x - 2} \).
Đề 13
Câu 1 (3,0 điểm):
a) Nêu điều kiệnđể \(\sqrt A \) có nghĩa.
Áp dụng: Tìm điều kiện của \(x\) để \(\sqrt {3x - 7} \) có nghĩa.
b) Tính: \(\dfrac{1}{2}\sqrt {48} - 2\sqrt {75} + \dfrac{{\sqrt {33} }}{{\sqrt {11} }}.\)
c) Rút gọn biểu thức: \(P = \left( {\dfrac{{x\sqrt x - 1}}{{x - \sqrt x }} - \dfrac{{x\sqrt x + 1}}{{x + \sqrt x }}} \right):\left[ {\dfrac{{2\left( {x - 2\sqrt x + 1} \right)}}{{x - 1}}} \right]\) (với \(x > 0\)và \(x \ne 1\))
Câu 2 (3 điểm):
Cho hàm số \(y = 2x - 2\).
a) Hàm số đã cho đồng biến hay nghịch biến trên \(\mathbb{R}\). Vì sao?
b) Vẽ đồ thị hàm số \(y = 2x - 2\).
c) Với giá trị nào của \(m\) thì đường thẳng \(y = (m - 1)x + 3\,\,\,\,\,(m \ne 1)\) song song với đường thẳng \(y = 2x - 2\).
Câu 3 (1,0 điểm):
Giải hệ phương trình: \(\left\{ \begin{array}{l}3x + y = 3\\2x - y = 7\end{array} \right.\)
Câu 4 (1,0 điểm):
Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\), biết \(BH = 9cm,\,\,CH = 25cm\). Tính \(AH\).
Câu 5 (1 điểm):
Cho đường tròn \((O)\), điểm \(A\) nằm bên ngoài đường tròn. Kẻ các tiếp tuyến \(AM,AN\) với đường tròn (\(M,N\) là các tiếp điểm).
a) Chứng minh rằng \(OA \bot MN\).
b) Vẽ đường kính \(NOC\). Chứng minh rằng MC// AO.
Đề 14
Câu 1 (2,0 điểm):
a) Tính: \(3\sqrt {16} + 5\sqrt {36} \)
b) Chứng minh rằng: với \(x > 0\) và \(x \ne 1\) thì \(\dfrac{{\sqrt x }}{{\sqrt x - 1}} - \dfrac{1}{{x - \sqrt x }} = \dfrac{{\sqrt x + 1}}{{\sqrt x }}\)
Câu 2 (2,5 điểm) Cho hàm số \(y = (2m + 1)x - 6\) có đồ thị \((d)\).
a) Với giá trị nào của \(m\) thì hàm số nghịch biến trên \(R\).
b) Tìm \(m\) để đồ thị hàm số \((d)\) đã cho đi qua điểm \(A(1;\,\,2)\).
c) Vẽ \((d)\) khi \(m = - 2\).
Câu 3 (1,5 điểm):
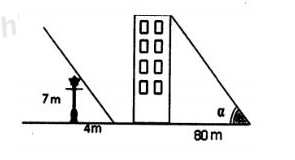
Một cột đèn cao \(7m\) có bóng trên mặt đất dài \(4m\). Gần đó có một tòa nhà cao tầng có bóng trên mặt đất dài \(80m\) (hình vẽ). Em hãy cho biết tòa nhà đó có bao nhiêu tầng, biết rằng mỗi tầng cao \(2m\).
Câu 4 (1,5 điểm):
Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) (\(H\) thuộc \(BC\)). Biết \(\angle ACB = {60^0},\,\,CH = a\). Tính độ dài \(AB\) và \(AC\) theo \(a\).
Câu 5 (3,0 điểm):
Cho tam giác \(ABC\) vuông tại \(A\,\,(AB < AC)\). Vẽ đường tròn tâm \(O\) đường kính \(AC\) cắt cạnh \(BC\) tại \(D\,\,(D \ne C)\). Gọi \(H\) và \(K\) lần lượt là trung điểm của \(AD\) và \(DC.\) Tia \(OH\) cắt cạnh \(AB\) tại \(E\) . Chứng minh:
a) \(AD\) là đường cao của tam giác \(ABC\).
b) \(DE\) là tiếp tuyến của đường tròn \((O)\).
c) Tứ giác \(OHDK\) là hình chữ nhật.
Đề 15
Bài 1 (1,0 điểm):
Giải phương trình \({x^2} + 28x - 128 = 0\)
Bài 2 (1,5 điểm):
Cho phương trình \((m + 1){x^2} - (2m + 3)x + m + 4 = 0\,\,\,\,\,(1)\), với \(m\) là tham số.
a) Giải phương trình khi \(m = - 1\) .
b) Tìm tất cả các giá trị của \(m\) để phương trình (1) có nghiệm.
Bài 3 (3,0 điểm):
Cho \((P)\) là đồ thị hàm số \(y = - \dfrac{1}{2}{x^2},\,\,\,(d)\) là đồ thị hàm số \(y = 2x\) và \((d')\) là đồ thị hàm số \(y = - x\).
a) Vẽ đồ thị của các hàm số \(y = - \dfrac{1}{2}{x^2},\,\,\,y = 2x,\,\,\,y = - x\) trên cùng một mặt phẳng tọa độ.
b) Các đồ thị \((P),\,\,(d)\,\)và \(\,(d')\) có một điểm chung là gốc tọa độ\(O\). Gọi \(A\) là giao điểm thứ hai của \((P)\) và \((d)\), gọi \(B\) là giao điểm thứ hai của \((P)\) và \((d')\). Chứng minh rằng tam giác \(OAB\) vuông và tính diện tích tam giác \(OAB\) (đơn vị đo trên các trục tọa độ là xentimét).
Bài 4 (1,0 điểm):
Tìm hai số tự nhiên, biết rằng hiệu của số lớn và số nhỏ bằng \(1814\) và nếu lấy số lớn chia cho số nhỏ thì được thương là \(9\) và số dư là \(182\).
Bài 5 (3,5 điểm):
Cho góc \(\widehat {xAy} = {60^0}\) và \((O)\) là đường tròn tiếp xúc với tia \(Ax\) tại \(B\) và tiếp xúc với tia \(Ay\) tại \(C\). Trên cung nhỏ của đường tròn \((O)\) lấy điểm \(M\) và gọi \(D,\,\,E,\,\,F\) lần lượt là hình chiếu vuông góc của \(M\) trên \(BC,\,\,CA,\,\,AB\).
a) Chứng minh tứ giác \(CDME\) là tứ giác nội tiếp.
b) Tính số đo của góc \(\widehat {EDF}\).
c) Chứng minh rằng \(M{D^2} = ME.MF\).
Đề 16
Câu 1 (1,5 điểm): Thực hiện phép tính
a) \(2\sqrt {50} - 3\sqrt {32} - \sqrt {162} + 5\sqrt {98} \)
b) \(\sqrt {8 + 2\sqrt 7 } + \sqrt {11 - 4\sqrt 7 } \)
c) \(\dfrac{{10}}{{\sqrt 5 }} + \dfrac{8}{{3 + \sqrt 5 }} - \dfrac{{\sqrt {18} - 3\sqrt 5 }}{{\sqrt 2 - \sqrt 5 }}\)
Câu 2 (2,0 điểm): Cho biểu thức \(P = \left( {\dfrac{{2\sqrt x }}{{\sqrt x + 3}} + \dfrac{{\sqrt x }}{{\sqrt x - 3}} - \dfrac{{3x + 3}}{{x - 9}}} \right):\left( {\dfrac{{2\sqrt x - 2}}{{\sqrt x - 3}} - 1} \right)\), với \(x \ge 0\)và \(x \ne 9\)
a) Rút gọn P.
b) Tìm x để P đạt giá trị nhỏ nhất.
Câu 3 (1,5 điểm): Cho hàm số\(y = 0,5x\) có đồ thị là \(\left( {{d_1}} \right)\)và hàm số \(y = - x + 3\) có đồ thị là \(\left( {{d_2}} \right)\).
a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ Oxy .
b) Xác định các hệ số a, b của đường thẳng \(\left( {{d_3}} \right)\)\(:\,\,y = ax + b\). Biết \(\left( {{d_3}} \right)\) song song với \(\left( {{d_1}} \right)\) và \(\left( {{d_3}} \right)\) cắt \(\left( {{d_2}} \right)\) tại một điểm có hoành độ bằng 4.
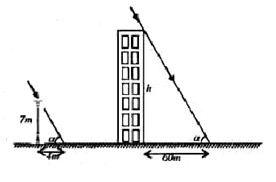
Câu 4 (4,5 điểm):1. Một cột đèn cao 7 m có bóng trên mặt đất 4 m . Cùng thời điểm đó, một tòa nhà cao tầng có bóng trên mặt đất là 60 m . Hãy cho biết tòa nhà đó cao bao nhiêu tầng, biết rằng mỗi tầng cao 3 m . (Hình vẽ minh họa)
2. Cho \(\Delta ABC\,\,(AB < AC)\) nội tiếp đường tròn \(\left( O \right)\)có BC là đường kính, vẽ đường cao AH của \(\Delta ABC\). \((H \in BC)\)
a) Biết \(AB = 6cm,\,\,AC = 8cm\). Tính độ dài AH và HB .
b) Tiếp tuyến tại A của \(\left( O \right)\) cắt các tiếp tuyến tại B và C lần lượt tại M và N . Chứng minh \(MN = MB + NC\) và \(\angle MON = {90^o}\).
c) Trên cạnh AC lấy điểm E sao cho \(AB = AE\), gọi I là trung điểm của BE . Chứng minh 3 điểm M, I, O thẳng hàng.
d) Chứng minh HI là tia phân giác của \(\angle AHC\).
Câu 5 (0,5 điểm): Xe lăn cho người khuyết tật.

Với sự phát triển của khoa học kỹ thuật hiện nay, người ta tạo ra nhiều mẫu xe lăn đẹp và tiện dụng cho người khuyết tật. Công ty A đã sản xuất ra những chiếc xe lăn cho người khuyết tật với số vốn ban đầu là 500 triệu đồng ( dùng để mua nguyên vật liệu và thiết bị sản xuất ). Chi phí để sản xuất ra một chiếc xe lăn là 2,5 triệu đồng. Giá bán ra thị trường mỗi chiếc là 3 triệu đồng.
a) Em hãy viết hàm số biểu diễn tổng số tiền đã đầu tư đến khi sản xuất ra được x chiếc xe lăn ( gồm vốn ban đầu và chi phí sản xuất ) và hàm số biểu diễn số tiền thu được khi bán ra x chiếc xe lăn.
b) Công ty A phải bán bao nhiêu chiếc xe lăn với giá trên mới có thể thu hồi được đủ số tiền vốn đã đầu tư ban đầu? ( Gồm vốn ban đầu và chi phí sản xuất )
Đề 17
I. TRẮC NGHIỆM (1 điểm) Trả lời câu hỏi bằng cách viết lại chữ cái trước đáp án đúng vào bài làm:
Câu 1 : Nếu x thỏa mãn điều kiện \(\sqrt {3 + \sqrt x } = 2\) thì x nhận giá trị là:
A. 0 B. 4
C. 5 D. 1
Câu 2 : Điều kiện để hàm số bậc nhất \(y = \left( {1 - m} \right)x + m\,\,\left( {m \ne 1} \right)\)là hàm số nghịch biến là:
A. \(m > 1\) B. \(m \ge 1\)
C. \(m \le 1\) D. \(m < 1\)
Câu 3 : Cho tam giác MNP vuông tại M , đường cao MH . Chọn hệ thức sai:
A. \(M{H^2} = HN.HP\)
B. \(M{P^2} = NH.HP\)
C. \(MH.NP = MN.MP\)
D. \(\dfrac{1}{{M{N^2}}} + \dfrac{1}{{M{P^2}}} = \dfrac{1}{{M{H^2}}}\)
Câu 4 : Cho hai đường tròn \(\left( {I;7cm} \right)\)và \(\left( {K;5cm} \right)\). Biết \(IK = 2cm\). Quan hệ giữa hai đường tròn là:
A. Tiếp xúc trong
B. Tiếp xúc ngoài
C. Cắt nhau
D. Đựng nhau
II. TỰ LUẬN (9 điểm)
Câu 1 (1 điểm): Thực hiện phép tính: a) \(3\sqrt {\dfrac{1}{3}} + 4\sqrt {12} - 5\sqrt {27} \) b) \(\dfrac{{3 + 2\sqrt 3 }}{{\sqrt 3 }} - \dfrac{2}{{\sqrt 3 - 1}}\)
Câu 2 (2 điểm): Cho biểu thức \(P = \dfrac{{\sqrt x }}{{\sqrt x - 2}} + \dfrac{{\sqrt x }}{{\sqrt x + 2}} - \dfrac{{x - 2\sqrt x }}{{x - 4}}\) và \(Q = \dfrac{{\sqrt x + 2}}{{\sqrt x - 2}}\,\,\left( {x \ge 0;x \ne 4} \right)\)
a) Rút gọn P
b) Tìm x sao cho \(P = 2\)
c) Biết \(M = P:Q\). Tìm giá trị của x để \({M^2} < \dfrac{1}{4}\)
Câu 3 (2 điểm): Cho hàm số \(y = \left( {m - 4} \right)x + 4\) có đồ thị là đường thẳng \(\left( d \right)\)\(\left( {m \ne 4} \right)\).
a) Tìm m để đồ thị hàm số đi qua \(A\left( {1;6} \right)\)
b) Vẽ đồ thị hàm số với m tìm được ở câu a. Tính góc tạo bởi đồ thị hàm số vừa vẽ với trục Ox (làm tròn đến phút).
c) Tìm m để đường thẳng \(\left( d \right)\) song song với đường thẳng\(\left( {{d_1}} \right):y = \left( {m - {m^2}} \right)x + m + 2\)
Câu 4 (3,5 điểm): Cho đường tròn \(\left( {O;R} \right)\) và điểm A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AE đến đường tròn \(\left( O \right)\) (với E là tiếp điểm). Vẽ dây EH vuông góc với AO tại M .
a) Cho biết bán kính \(R = 5cm,\,\,OM = 3cm\). Tính độ dài dây EH .
b) Chứng minh AH là tiếp tuyến của đường tròn\(\left( O \right)\).
c) Đường thẳng qua O vuông góc với OA cắt AH tại B . Vẽ tiếp tuyến BF với đường tròn \(\left( O \right)\) ( F là tiếp điểm). Chứng minh 3 điểm E, O, F thẳng hàng và \(BF.AE = {R^2}\).
d) Trên tia HB lấy điểm I (\(I \ne B\)), qua I vẽ tiếp tuyến thứ hai với đường tròn \(\left( O \right)\) cắt các đường thẳng BF, AE lần lượt tại C và D . Vẽ đường thẳng IF cắt AE tại Q . Chứng minh \(AE = DQ\).
Câu 5 (0,5 điểm): Cho x,y là các số thực dương thỏa mãn \(x + y \le 1\).
Tìm giá trị nhỏ nhất của biểu thức \(P = \left( {\dfrac{1}{x} + \dfrac{1}{y}} \right).\sqrt {1 + {x^2}{y^2}} \).
Đề 18
Câu 1 (2 điểm):
Cho \(A = \left( {\dfrac{{x + \sqrt x + 10}}{{x - 9}} + \dfrac{1}{{3 - \sqrt x }}} \right):\dfrac{1}{{\sqrt x - 3}}\)và \(B = \sqrt x + 1\) (với \(x \ge 0;\,\,x \ne 9\))
a) Tính giá trị của biểu thức B khi \(x = 16\)
b) Rút gọn A
c) Tìm giá trị của x để \(A > B\)
Câu 2 (2 điểm):
Cho đường thẳng \(\left( d \right)\) có phương trình \(y = \left( {2k - 1} \right)x + k - 2\)(với k là tham số)
a) Tìm giá trị của k biết đường thẳng \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right)\) có phương trình \(y = - 3x + 5\)
b) Với giá trị của k tìm được ở câu a, vẽ đường thẳng \(\left( d \right)\) trên mặt phẳng tọa độ và tính khoảng cách từ gốc tọa độ O đến đường thẳng \(\left( d \right)\)
Câu 3 (2điểm): Giải phương trình
a) \(\sqrt {x + 3} + \sqrt {16x + 48} = 6 + \sqrt {9x + 27} \)
b) \(\sqrt {4x + 1} = x - 1\)
Câu 4 (3,5 điểm): Cho đường tròn \(\left( {O,R} \right)\). Đường thẳng d không qua O cắt \(\left( O \right)\) tại hai điểm A và B . Điểm C thuộc tia đối của tia AB . Vẽ CE và CF là các tiếp tuyến của \(\left( O \right)\) ( E, F là hai tiếp điểm). Gọi H là trung điểm của AB .
a) Chứng minh 4 điểm C, E, O, H cùng thuộc một đường tròn.
b) Gọi CO cắt EF tại K . Chứng minh \(OK.OC = {R^2}\)
c) Đoạn thẳng CO cắt \(\left( O \right)\) tại I . Chứng minh I là tâm đường tròn nội tiếp tam giác CEF
d) Tìm vị trí điểm C trên tia đối của tia AB để tam giác CEF đều.
Câu 5 (0,5 điểm):
Cho \(0 < x < 1\). Tìm giá trị nhỏ nhất của biểu thức
\(M = \dfrac{x}{{1 - x}} + \dfrac{4}{x}\)
Đề 19
Phần I: Trắc nghiệm khách quan (2,0 điểm)
Học sinh ghi đáp án đúng là A, B, C hoặc D vào tờ giấy thi
1 . Điều kiện xác định của biểu thức\(\sqrt {6 - 3x} \) là:
A. \(x \le 2\) B. \(x \ge 2\)
C. \(x \ge 0\) D. \(x < 2\)
2 . Giá trị nhỏ nhất của biểu thức \(p = \sqrt {x + 3} - 1\) là:
A. \(3\) B. \( - 1\)
C. \( - 3\) D. \(0\)
3 . Giá trị biểu thức \(P = \dfrac{{\sqrt x - 3}}{{\sqrt x + 3}}\)khi \(x = 4 - 2\sqrt 3 \) là:
A. \( - 11 + 6\sqrt 3 \) B. \(\dfrac{{ - 11 - 6\sqrt 3 }}{{13}}\)
C. \(\dfrac{{ - 5 - 12\sqrt 3 }}{{37}}\) D. \(1\)
4 . Cho tam giác ABC vuông tại A . Biết rằng \(\dfrac{{AB}}{{AC}} = \sqrt 3 \). Số đo độ của góc ABC bằng:
A. \({30^0}\) B. \({60^0}\)
C. \({45^0}\) D. \({50^0}\)
5 . Với giá trị nào của a thì hàm số \(y = \left( {a - 5} \right)x + 1\) đồng biến trên tập\(\mathbb{R}\)?
A. \(a < 5\) B. \(a > 5\)
C. \(a = 5\) D. \(a > - 5\)
6 . Cho hai đường thẳng\(\left( {{d_1}} \right)\)\(:\,\,y = 2x + 3\) và\(\left( {{d_2}} \right)\)\(:\,\,y = \left( {{m^2} + 1} \right)x + m + 2\) (với m là tham số). Với giá trị nào của tham số m thì đường thẳng \(\left( {{d_1}} \right)\) song song với đường thẳng \(\left( {{d_2}} \right)\)?
A. \(m = 2\)
B. \(m = 1\) hoặc\(m = - 1\)
C. \(m = 1\)
D. \(m = - 1\)
7 . Cho EM, EN là hai tiếp tuyến của đường tròn \(\left( O \right)\) với tiếp điểm M, N . Khẳng định nào sau đây là sai:
A. \(\angle EMO = {90^o}\)
B. Bốn điểm E, M, O, N cùng thuộc một đườngtròn
C. MN là trung trực của EO
D. OE là phân giác của\(\angle MON\)
8 . Hai đường tròn \(\left( {O;5} \right)\)và \(\left( {O';8} \right)\) có vị trí tương đối với nhau như thế nào biết \(OO' = 12\)
A. Tiếp xúc nhau
B. Không giao nhau
C. Tiếp xúc ngoài
D. Cắt nhau
Phần II: Tự luận (8,0 điểm)
Câu 1 (2,0 điểm): Cho hai biểu thức \(A = \dfrac{{2\sqrt x }}{{\sqrt x + 3}} + \dfrac{{\sqrt x }}{{\sqrt x - 3}} - \dfrac{{3x + 3}}{{x - 9}}\)và \(B = \dfrac{{\sqrt x + 1}}{{\sqrt x - 3}}\) với \(x \ge 0\,,\,\,x \ne 9\)
1) Rút gọn biểu thức A .
2) Tìm tất cả các giá trị của x để \(\dfrac{A}{B} < - \dfrac{1}{2}\).
Câu 2 (2,5 điểm): Trong mặt phẳng tọa độ Oxy , cho đường thẳng \(\left( d \right)\)\(:\,\,y = ax + 3\).
1) Xác định a biết \(\left( d \right)\) đi qua \(K\left( {1; - 1} \right)\). Vẽ đồ thị với a vừa tìm được.
2) Tìm tất cả các giá trị của a để đường thẳng \(\left( d \right)\) cắt Ox và Oy lần lượt tại hai điểm M và N sao cho diện tích tam giác OMN bằng 4.
Câu 3 (3,0 điểm): Cho đường tròn \(\left( {O;R} \right)\). Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF đến đường tròn (với E, F là các tiếp điểm).
1) Chứng minh các điểm M, E, O, F cùng thuộc một đường tròn.
2) Đoạn OM cắt đường tròn \(\left( {O;R} \right)\) tại I . Chứng minh I là tâm đường tròn nội tiếp tam giác MEF .
3) Kẻ đường kính ED của \(\left( {O;R} \right)\). Hạ FK vuông góc với ED . Gọi P là giao điểm của MD và FK . Chứng minh P là trung điểm của FK .
Câu 4 (0,5 điểm): Giải phương trình \({x^2} + x - 17 = \sqrt {\left( {{x^2} - 15} \right)\left( {x - 3} \right)} + \sqrt {{x^2} - 15} + \sqrt {x - 3} \)
Đề bài
Câu 1 (2,5 điểm): Cho hai biểu thức: \(A\, = \,\dfrac{{2\sqrt x - 4}}{{\sqrt x - 1}}\) và \(B\, = \,\dfrac{{\sqrt x }}{{\sqrt x - 1}} + \dfrac{3}{{\sqrt x + 1}} - \dfrac{{6\sqrt x - 4}}{{x - 1}}\) với \(x \ge 0,\,\,x \ne 1.\)
1. Tính giá trị của A khi \(x = 4.\)
2. Rút gọn B .
3. So sánh A.B với 5.
Câu 2 (2,0 điểm):
1. Thực hiện phép tính: \(\left( {3\sqrt 8 - \sqrt {18} + 5\sqrt {\dfrac{1}{2}} + \sqrt {50} } \right).3\sqrt 2 .\)
2. Giải phương trình: \(\sqrt {4{x^2} - 4x + 1} - 5 = 2.\)
Câu 3 (1,5 điểm): Cho hàm số \(y = 3x + 2\) có đồ thị là đường thẳng \(\left( {{d_1}} \right).\)
1. Điểm \(A\left( {\dfrac{1}{3};3} \right)\) có thuộc đường thẳng \(\left( {{d_1}} \right)\) không? Vì sao?
2. Tìm giá trị của \(m\) để đường thẳng \(\left( {{d_1}} \right)\) và đường thẳng \(\left( {{d_2}} \right)\) có phương trình \(y = - 2x - m\) cắt nhau tại điểm có hoành độ bằng 1.
Câu 4 (3,5 điểm): Cho đường tròn \(\left( {O;R} \right)\) đường kính AB và điểm C bất kỳ thuốc đường tròn ( C khác A và B ). Kẻ tiếp tuyến tại A của đường tròn, tiếp tuyến này cắt tia BC ở D . Đường thẳng tiếp xúc với đường tròn tại C cắt AD ở E .
1. Chứng minh bốn điểm A,E,C,O cùng thuộc một đường tròn.
2. Chứng minh \(BC.BD = 4{R^2}\) và OE song song với BD .
3. Đường thẳng kẻ qua O và vuông góc với BC tại N cắt tia EC ở F . Chứng minh BF là tiếp tuyến của đường tròn \(\left( {O;R} \right)\)
4. Gọi H là hình chiếu của C trên AB , M là giao của AC và OE . Chứng minh rằng khi điểm C di động trên đường tròn \(\left( {O;R} \right)\) và thỏa mãn yêu cầu đề bài thì đường tròn ngoại tiếp tam giác HMN luôn đi qua một điểm cố định.
Câu 5 (0,5 điểm):
Tìm giá trị nhỏ nhất của biểu thức \(P = x + \dfrac{9}{{x - 2}} + 2010\) với \(x > 2.\)