Đề kiểm tra 15 phút chương 2: Hàm số bậc nhất - Đề số 1
Đề bài
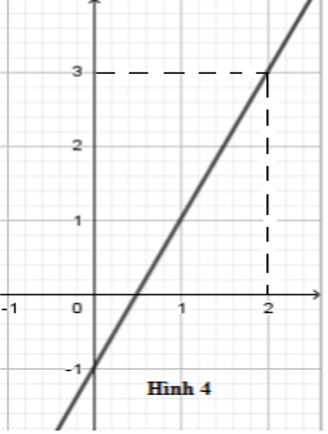
Hình vẽ bên là đồ thị của hàm số nào dưới đây?
-
A.
\(y = 2x - 1\)
-
B.
\(y = x - 1\)
-
C.
\(y = x - 2\)
-
D.
\(y = - 2x - 1\)
Chọn đáp án đúng nhất. Hàm số $y = ax + b$ là hàm số bậc nhất khi
-
A.
$a = 0$
-
B.
$a < 0$
-
C.
$a > 0$
-
D.
$a \ne 0$
Hàm số \(y = \dfrac{{3m}}{{1 - 2m}}x - 5\) là hàm số bậc nhất khi:
-
A.
\(m \notin \left\{ {0;\dfrac{1}{2}} \right\}\)
-
B.
\(m > 0\)
-
C.
\(m \ne 0\)
-
D.
\(m \ne \dfrac{1}{2}\)
Đồ thị hàm số $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ đi qua điểm nào dưới đây?
-
A.
$A\left( {\dfrac{{ - 5}}{3};0} \right)$
-
B.
$B\left( {1;\dfrac{3}{4}} \right)$
-
C.
$C\left( { \dfrac{2}{3};\dfrac{1}{3}} \right)$
-
D.
$D\left( {4;\dfrac{4}{3}} \right)$
Hàm số nào sau đây là hàm số nghịch biến?
-
A.
$y = 2x - 1$
-
B.
$y = - \left( {1 - 3x} \right)$
-
C.
$y = - \left( {2x - 1} \right)$
-
D.
$y = x$
Cho hàm số $y = \sqrt {{m^2} + 3} .x + 1$. Kết luận nào sau đây là đúng?
-
A.
Hàm số đã cho là hàm nghịch biến với mọi $m$
-
B.
Hàm số đã cho là hàm nghịch biến với $m > \sqrt 3 $
-
C.
Hàm số đã cho là hàm hằng
-
D.
Hàm số đã cho là hàm số đồng biến với mọi $m$
Cho hàm số \(y = \left( {5 - \sqrt {5 - m} } \right).x + m + 2\). Với giá trị nguyên lớn nhất của \(m\) để hàm số nghịch biến là?
-
A.
\(m = 5\)
-
B.
\(m = - 20\)
-
C.
\(m = - 19\)
-
D.
\(m = - 21\)
Cho hàm số \(y = \left( {\dfrac{m}{2} - 3} \right)x + m + 1\). Tìm \(m\) để hàm số là hàm số nghịch biến
-
A.
\(m > 6\)
-
B.
\(m = 6\)
-
C.
\(m < 6\)
-
D.
\(m \ne 6\)
Cho đường thẳng \({d_1}:y = \dfrac{{4 - x}}{3}\) và \({d_2}:y = 8 - 2x\). Gọi \(A,B\) lần lượt là giao điểm của \({d_1}\) với \({d_2}\) và \({d_1}\) với trục tung. Tổng tung độ giao điểm của \(A\) và \(B\) là
-
A.
\(\dfrac{4}{3}\)
-
B.
\(\dfrac{2}{3}\)
-
C.
\(9\)
-
D.
\(8\)
Cho đường thẳng \(d:y = - 3x + 2\) . Gọi \(A,B\) lần lượt là giao điểm của \(d\) với trục hoành và trục tung. Tính diện tích tam giác \(OAB\)
-
A.
\(\dfrac{4}{3}\)
-
B.
\( - \dfrac{2}{3}\)
-
C.
\(\dfrac{3}{2}\)
-
D.
\(\dfrac{2}{3}\)
Cho ba đường thẳng \({d_1}:y = - x + 5;{d_2}:y = 5x - 1;{d_3}:y = - 2x + 6\). Khẳng định nào dưới đây là đúng?
-
A.
Giao điểm của \({d_1}\) và \({d_2}\) là \(M\left( {0;5} \right)\).
-
B.
Ba đường thẳng trên đồng quy tại \(N\left( {1;4} \right)\)
-
C.
Ba đường thẳng trên không đồng quy
-
D.
Ba đường thẳng trên đồng quy tại điểm \(M\left( {0;5} \right)\).
Lời giải và đáp án
Hình vẽ bên là đồ thị của hàm số nào dưới đây?

-
A.
\(y = 2x - 1\)
-
B.
\(y = x - 1\)
-
C.
\(y = x - 2\)
-
D.
\(y = - 2x - 1\)
Đáp án : A
Sử dụng cách vẽ đồ thị hàm số
Đồ thị hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\) là một đường thẳng
Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b),\,\,B\left( { - \dfrac{b}{a};0} \right).\)
Từ hình vẽ suy ra đồ thị hàm số đi qua hai điểm có tọa độ \(\left( {0; - 1} \right)\) và \(\left( {2;3} \right)\) .
Thay tọa độ hai điểm vào mỗi hàm số ta thấy với hàm số \(y = 2x - 1\)
+) Thay \(x = 0;y = - 1\) và vào hàm số \(y = 2x - 1\) ta được \( - 1 = 2.0 - 1 \Leftrightarrow - 1 = - 1\) (luôn đúng)
+) Thay \(x = 2;y = 3\) và vào hàm số \(y = 2x - 1\) ta được \(3 = 2.2 - 1 \Leftrightarrow 3 = 3\) (luôn đúng)
Vậy đồ thị hàm số \(y = 2x - 1\) là đường thẳng như hình vẽ.
Chọn đáp án đúng nhất. Hàm số $y = ax + b$ là hàm số bậc nhất khi
-
A.
$a = 0$
-
B.
$a < 0$
-
C.
$a > 0$
-
D.
$a \ne 0$
Đáp án : D
Hàm số bậc nhất là hàm số có dạng $y = ax + b\,\,\left( {a \ne 0} \right)$.
Hàm số \(y = \dfrac{{3m}}{{1 - 2m}}x - 5\) là hàm số bậc nhất khi:
-
A.
\(m \notin \left\{ {0;\dfrac{1}{2}} \right\}\)
-
B.
\(m > 0\)
-
C.
\(m \ne 0\)
-
D.
\(m \ne \dfrac{1}{2}\)
Đáp án : A
Sử dụng định nghĩa hàm số bậc nhất
Hàm số bậc nhất là hàm số dạng \(y = ax + b\,\,\left( {a \ne 0} \right)\)
Hàm số \(y = \dfrac{{3m}}{{1 - 2m}}x - 5\) là hàm số bậc nhất khi \(\left\{ \begin{array}{l}\dfrac{{3m}}{{1 - 2m}} \ne 0\\1 - 2m \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3m \ne 0\\2m \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne \dfrac{1}{2}\end{array} \right.\)
Đồ thị hàm số $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ đi qua điểm nào dưới đây?
-
A.
$A\left( {\dfrac{{ - 5}}{3};0} \right)$
-
B.
$B\left( {1;\dfrac{3}{4}} \right)$
-
C.
$C\left( { \dfrac{2}{3};\dfrac{1}{3}} \right)$
-
D.
$D\left( {4;\dfrac{4}{3}} \right)$
Đáp án : C
Đồ thị hàm số \(y = ax + b(a \ne 0)\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) khi và chỉ khi \({y_0} = a{x_0} + b\)
Thay tọa độ từng điểm vào hàm số ta được
+) Với $A\left( {\dfrac{{ - 5}}{3};0} \right)$. Thay $x = - \dfrac{5}{3};y = 0$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( { - \dfrac{5}{3} - 1} \right) + \dfrac{4}{3} = 0 \Leftrightarrow \dfrac{{ - 20}}{3} = 0$ (Vô lý)
+) Với $B\left( {1;\dfrac{3}{4}} \right)$. Thay $x = 1;y = \dfrac{3}{4}$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( {1 - 1} \right) + \dfrac{4}{3} = \dfrac{3}{4} \Leftrightarrow \dfrac{4}{3} = \dfrac{3}{4}$ (Vô lý)
+) Với $D\left( {4;\dfrac{4}{3}} \right)$. Thay $x = 4;y = \dfrac{4}{3}$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( {4 - 1} \right) + \dfrac{4}{3} = \dfrac{4}{3} \Leftrightarrow \dfrac{{31}}{3} = \dfrac{4}{3}$ (Vô lý)
+)Với $C\left( { \dfrac{2}{3};\dfrac{1}{3}} \right)$. Thay $x = \dfrac{2}{3};y = \dfrac{1}{3}$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( { \dfrac{2}{3} - 1} \right) + \dfrac{4}{3} = \dfrac{1}{3} \Leftrightarrow \dfrac{1}{3} = \dfrac{1}{3}$ (luôn đúng)
$ \Rightarrow C$ thuộc đồ thị hàm số $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$
Hàm số nào sau đây là hàm số nghịch biến?
-
A.
$y = 2x - 1$
-
B.
$y = - \left( {1 - 3x} \right)$
-
C.
$y = - \left( {2x - 1} \right)$
-
D.
$y = x$
Đáp án : C
Hàm số bậc nhất $y = ax + b$ $(a \ne 0)$ xác định với mọi giá trị của $x$ thuộc \(\mathbb{R}\) và có tính chất sau:
- Đồng biến trên \(\mathbb{R}\) nếu \(a > 0\).
- Nghịch biến trên \(\mathbb{R}\) nếu \(a < 0\).
Hàm số $y = 2x - 1$có $a = 2 > 0$ nên là hàm số đồng biến
Hàm số $y = - \left( {1 - 3x} \right)$$ \Leftrightarrow y = 3x - 1$ có $a = 3 > 0$ nên là hàm số đồng biến
Hàm số $y = - \left( {2x - 1} \right)$$ \Leftrightarrow y = - 2x + 1$có $a = - 2 < 0$ nên là hàm số nghịch biến
Hàm số $y = x$ có $a = 1 > 0$ nên là hàm số đồng biến
Cho hàm số $y = \sqrt {{m^2} + 3} .x + 1$. Kết luận nào sau đây là đúng?
-
A.
Hàm số đã cho là hàm nghịch biến với mọi $m$
-
B.
Hàm số đã cho là hàm nghịch biến với $m > \sqrt 3 $
-
C.
Hàm số đã cho là hàm hằng
-
D.
Hàm số đã cho là hàm số đồng biến với mọi $m$
Đáp án : D
Sử dụng tính chất :
Hàm số bậc nhất $y = ax + b$ $(a \ne 0)$ xác định với mọi giá trị của $x$ thuộc \(\mathbb{R}\) và có tính chất sau
- Đồng biến trên \(\mathbb{R}\) nếu \(a > 0\).
- Nghịch biến trên \(\mathbb{R}\) nếu \(a < 0\).
Hàm số $y = \sqrt {{m^2} + 3} .x + 1$ có ${m^2} + 3 \ge 3 > 0$ với mọi $m$ nên là hàm số đồng biến với mọi $m$.
Cho hàm số \(y = \left( {5 - \sqrt {5 - m} } \right).x + m + 2\). Với giá trị nguyên lớn nhất của \(m\) để hàm số nghịch biến là?
-
A.
\(m = 5\)
-
B.
\(m = - 20\)
-
C.
\(m = - 19\)
-
D.
\(m = - 21\)
Đáp án : D
-Sử dụng tính chất :
Hàm số bậc nhất \(y = ax + b\) \(\left( {a \ne 0} \right)\) xác định với mọi giá trị của \(x\) thuộc \(\mathbb{R}\) và có tính chất sau
+ Đồng biến trên \(\mathbb{R}\) nếu \(a > 0\).
+ Nghịch biến trên \(\mathbb{R}\) nếu \(a < 0\).
- Giải bất phương trình chứa căn dạng \(\sqrt A > b\,\left( {b \ge 0} \right) \Leftrightarrow \left\{ \begin{array}{l}A \ge 0\\A > {b^2}\end{array} \right.\).
Hàm số \(y = \left( {5 - \sqrt {5 - m} } \right).x + m + 2\) là hàm số nghịch biến khi \(5 - \sqrt {5 - m} < 0\)
ĐK: \(5 - m \ge 0 \Leftrightarrow m \le 5\)
Khi đó \(5 - \sqrt {5 - m} < 0 \Leftrightarrow \sqrt {5 - m} > 5\)\( \Rightarrow 5 - m > 25 \Leftrightarrow m < - 20\)
Kết hợp điều kiện ta được \(m < - 20\) nên giá trị nguyên lớn nhất của \(m\) thỏa mãn là \(m = - 21.\)
Cho hàm số \(y = \left( {\dfrac{m}{2} - 3} \right)x + m + 1\). Tìm \(m\) để hàm số là hàm số nghịch biến
-
A.
\(m > 6\)
-
B.
\(m = 6\)
-
C.
\(m < 6\)
-
D.
\(m \ne 6\)
Đáp án : C
Hàm số bậc nhất \(y = ax + b\) \(\left( {a \ne 0} \right)\) xác định với mọi giá trị của \(x\) thuộc \(\mathbb{R}\) và có tính chất sau
- Đồng biến trên \(\mathbb{R}\) nếu \(a > 0\).
- Nghịch biến trên \(\mathbb{R}\) nếu \(a < 0\).
Hàm số \(y = \left( {\dfrac{m}{2} - 3} \right)x + m + 1\) là hàm số nghịch biến khi \(\dfrac{m}{2} - 3 < 0 \Leftrightarrow \dfrac{m}{2} < 3 \Leftrightarrow m < 6\).
Cho đường thẳng \({d_1}:y = \dfrac{{4 - x}}{3}\) và \({d_2}:y = 8 - 2x\). Gọi \(A,B\) lần lượt là giao điểm của \({d_1}\) với \({d_2}\) và \({d_1}\) với trục tung. Tổng tung độ giao điểm của \(A\) và \(B\) là
-
A.
\(\dfrac{4}{3}\)
-
B.
\(\dfrac{2}{3}\)
-
C.
\(9\)
-
D.
\(8\)
Đáp án : A
Tìm tọa độ giao điểm của hai đường thẳng theo các bước
Bước 1. Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.
Bước 2. Thay hoành độ giao điểm vừa tìm được vào một trong hai phương trình đường thẳng ta tìm được tung độ giao điểm.
+) Phương trình hoành độ giao điểm của \({d_1}\) và \({d_2}\) là \(\dfrac{{4 - x}}{3} = 8 - 2x \Leftrightarrow 24 - 6x = 4 - x \Leftrightarrow 5x = 20 \Leftrightarrow x = 4\)\( \Rightarrow y = 0\) nên \(A\left( {4;0} \right)\)
+) \(B\left( {0;{y_B}} \right)\) là giao điểm của đường thẳng \({d_1}\) và trục tung. Khi đó ta có \({y_B} = \dfrac{{4 - 0}}{3} \Rightarrow {y_B} = \dfrac{4}{3}\).
Suy ra tổng tung độ \({y_A} + {y_B} = 0 + \dfrac{4}{3} = \dfrac{4}{3}.\)
Cho đường thẳng \(d:y = - 3x + 2\) . Gọi \(A,B\) lần lượt là giao điểm của \(d\) với trục hoành và trục tung. Tính diện tích tam giác \(OAB\)
-
A.
\(\dfrac{4}{3}\)
-
B.
\( - \dfrac{2}{3}\)
-
C.
\(\dfrac{3}{2}\)
-
D.
\(\dfrac{2}{3}\)
Đáp án : D
Bước 1. Tìm tọa độ giao điểm \(A,B\) .
Bước 2. Sử dụng công thức tính diện tích tam giác \(OAB\) vuông tại \(O\): \({S_{OAB}} = \dfrac{{OA.OB}}{2}\)
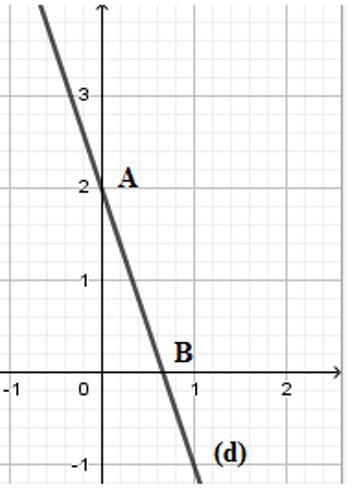
\(B\left( {x;0} \right)\) là giao điểm của \(d\) với trục hoành nên \(0 = - 3x + 2 \Leftrightarrow x = \dfrac{2}{3} \Rightarrow B\left( {\dfrac{2}{3};0} \right)\)
\(A\left( {0;y} \right)\) là giao điểm của \(d\) với trục tung nên \(y = - 3.0 + 2 \Leftrightarrow y = 2 \Rightarrow A\left( {0;2} \right)\).
Suy ra \(OA = \left| 2 \right| = 2;OB = \left| {\dfrac{2}{3}} \right| = \dfrac{2}{3}\).
Vì tam giác \(OAB\) vuông tại \(O\) nên \({S_{OAB}} = \dfrac{{OA.OB}}{2} = \dfrac{{2.\dfrac{2}{3}}}{2} = \dfrac{2}{3}\) (đvdt)
Cho ba đường thẳng \({d_1}:y = - x + 5;{d_2}:y = 5x - 1;{d_3}:y = - 2x + 6\). Khẳng định nào dưới đây là đúng?
-
A.
Giao điểm của \({d_1}\) và \({d_2}\) là \(M\left( {0;5} \right)\).
-
B.
Ba đường thẳng trên đồng quy tại \(N\left( {1;4} \right)\)
-
C.
Ba đường thẳng trên không đồng quy
-
D.
Ba đường thẳng trên đồng quy tại điểm \(M\left( {0;5} \right)\).
Đáp án : B
+) Để xét tính đồng quy của ba đường thẳng cho trước, ta thực hiện các bước sau
Bước 1. Tìm tọa độ giao điểm của hai đường thẳng trong ba đường thẳng đã cho.
Bước 2. Kiểm tra xem nếu giao điểm vừa tìm được thuộc đường thằng còn lại thì kết luận ba đường thẳng đó đồng quy.
+) Thay tọa độ điểm \(M\left( {0;5} \right)\) vào phương trình đường thẳng \({d_2}\) ta được \(5 = 5.0 - 1 \Leftrightarrow 5 = - 1\) (vô lý )
Nên \(B \notin {d_2}\). Suy ra A,D sai.
+) Xét tính đồng quy của ba đường thẳng
* Phương trình hoành độ giao điểm của \({d_1}\) và \({d_2}\): \( - x + 5 = 5x - 1 \Leftrightarrow 6x = 6 \Leftrightarrow x = 1\)\( \Rightarrow y = - 1 + 5 \Leftrightarrow y = 4\)
Suy ra tọa độ giao điểm của \({d_1}\)và \({d_2}\) là \(\left( {1;4} \right)\).
* Thay \(x = 1;y = 4\) vào phương trình đường thẳng \({d_3}\) ta được \(4 = - 2.1 + 6 \Leftrightarrow 4 = 4\) (luôn đúng)
Vậy ba đường thẳng trên đồng quy tại điểm \(N\left( {1;4} \right)\).