Tổng hợp đề kiểm tra giữa học kì 1 Toán 9 có đáp án và lời giải chi tiết — Không quảng cáo

Đề 1

Câu 1 (2 điểm): Tìm $x$ để biểu thức sau xác định:

a) $\sqrt {x - 3}$                                                                    b) $\sqrt { - \frac{2}{{2x - 1}}}$

Câu 2 (2 điểm): Thực hiện phép tính:

a) $\sqrt 5 .\sqrt {45}$                                              b) $\sqrt {12}  - \sqrt {27}  + \sqrt 3$                                               c) $\sqrt {7 + 2\sqrt 6 }  - \sqrt {7 - 2\sqrt 6 }$

Câu 3 (2 điểm): Giải phương trình:

a) $\sqrt {3x - 2}  = 6$                                                           b) $\sqrt {{{\left( {x - 1} \right)}^2}}  = 5$

Câu 4 (3,5 điểm): Cho tam giác $ABC$ vuông tại $A,$ có $AB = 12cm,$ $AC = 16cm.$ Kẻ đường cao $AM.$ Kẻ $ME \bot AB.$

a) Tính $BC,\,\,\angle B,\,\,\angle C.$

b) Tính độ dài $AM,\,\,BM.$

c) Chứng minh $AE.AB = A{C^2} - M{C^2}.$

Câu 5 (0,5 điểm):

a) Với $a,\,\,b \ge 0.$ Chứng minh $a + b \ge 2\sqrt {ab} .$

b) Áp dụng tính giá trị lớn nhất của biểu thức $S = \sqrt {x - 2}  + \sqrt {y - 3} ,$ biết $x + y = 6.$

Đề 2

Câu 1 (2 điểm): Thực hiện phép tính:

a) $5\sqrt {12}  - \sqrt {27}  - 2\sqrt {75}  + \sqrt {48}$

b) $\frac{2}{{\sqrt {13}  - \sqrt {11} }} + \frac{5}{{4 + \sqrt {11} }} - \sqrt {52}$

c) $\sqrt {6 + 2\sqrt 5 }  + \sqrt {9 - 4\sqrt 5 }  - \sqrt {20}$

Câu 2 (2 điểm): Giải các phương trình sau:

a) $3\sqrt x  = \sqrt {16x}  - 5$

b) $\sqrt {4x - 8}  - \sqrt {9x - 18}  + 4\sqrt {\frac{{x - 2}}{{25}}}  =  - 3$

c) $x - \sqrt {5x + 4}  = 2$

Câu 3 (2 điểm): Cho biểu thức: $A = \frac{{\sqrt x  - 2}}{{\sqrt x  + 1}};$ $B = \frac{{\sqrt x }}{{\sqrt x  + 1}} - \frac{{\sqrt x  - 4}}{{1 - x}}\,\,\,\left( {x \ge 0,\,\,x \ne 1} \right).$

a) Tính giá trị của biểu thức $A$ khi $x = 25.$

b) Rút gọn biểu thức $B.$

c) Tìm $x$để $A:B < \frac{1}{2}.$

Câu 4 (3 điểm): Cho $\Delta ABC$ vuông tại $A,$ đường cao $AH,$ $AB = 6cm,$ $BC = 10\,cm.$

a) Giải tam giác vuông $ABC.$ ( kết quả làm tròn đến phút )

b) Kẻ tia phân giác góc $A$ cắt $BC$ tại $E.$ Tính $BE,\,\,AE.$

c) Gọi $M,\,\,N$ theo thứ tự là hình chiếu của $E$ trên $AB$ và $AC.$ Tính diện tích tứ giác $AMEN.$

Câu 5 (1 điểm):

a) Giải bài toán sau: ( kết quả làm tròn đến số thập phân thứ hai )

Để đo chiều rộng của một khúc sông $AH,$ người ta chọn hai vị trí $B,\,\,C$ cùng một bờ. Biết $BC = 60\,\,m,$ $\angle ACB = {38^0},$ $\angle ABC = {30^0}.$  Hãy tính chiều rộng $AH$ của khúc sông đó.

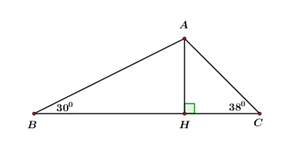
b) Tính giá trị nhỏ nhất của biểu thức $A = \sqrt {{{\left( {x - 2019} \right)}^2}}  + \sqrt {{{\left( {x - 2020} \right)}^2}} .$

Đề 3

Bài 1 (2 điểm): Tính giá trị của các biểu thức sau:

$A = \left( {\sqrt {99}  - \sqrt {18}  - \sqrt {11} } \right)\sqrt {11}  + 3\sqrt {22}$                                                 $B = \sqrt {4 + 2\sqrt 3 }  + \sqrt {4 - 2\sqrt 3 }$

$C = \frac{5}{{\sqrt 7  + \sqrt 2 }} + \frac{{7 - \sqrt 7 }}{{\sqrt 7  - 1}} + 6\sqrt {\frac{1}{2}}$

Bài 2 (2 điểm): Giải các phương trình sau:

a) $\sqrt {2x - 1}  = \sqrt {x + 1}$                                                                b) $\sqrt {4 - {x^2}}  - x + 2 = 0$

Bài 3 (2 điểm): Cho biểu thức $A = \frac{{\sqrt a  + 1}}{{\sqrt a  - 3}}$ và $B = \frac{{2\sqrt a }}{{\sqrt a  + 3}} - \frac{{\sqrt a }}{{3 - \sqrt a }} - \frac{{3a + 3}}{{a - 9}}\,\,\,\left( {a \ge 0,\,\,a \ne 9} \right).$

a) Tính giá trị của $A$ khi $a = 16.$                                                 b) Rút gọn biểu thức $P = \frac{A}{B}.$

c) So sánh $P$ với $1.$

Bài 4 (3,5 điểm):

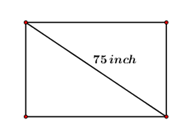
1. (1 điểm) Một chiếc tivi hình chữ nhật màn hình phẳng $75\,\,inch$ (đường chéo tivi dài $75\,\,inch$) có góc tạo với chiều rộng và đường chéo là ${53^0}08'.$ Hỏi chiếc tivi ấy có chiều dài, chiều rộng là bao nhiêu $cm?$ Biết $1\,inch = 2,54\,cm$ (kết quả làm tròn đến chữ số thập phân thứ nhất).

2. (2,5 điểm) Cho $\Delta EMF$ vuông tại $M$ có đường cao $MI.$ Vẽ $IP \bot ME\,\,\,\left( {P \in ME} \right),$ $IQ \bot MF\,\,\left( {Q \in MF} \right).$

a) Cho biết $ME = 4\,cm,\,\,\sin \angle MFE = \frac{3}{4}.$ Tính độ dài các đoạn $EF,\,\,EI,\,\,MI.$

b) Chứng minh $MP.PE + MQ.QF = M{I^2}.$

Bài 5 (0,5 điểm): Tìm giá trị nhỏ nhất của biểu thức $A = \sqrt {{x^2} + 6x + 9}  + \sqrt {{x^2} - 2x + 1} .$

Đề 4

Bài 1 (2 điểm):

Tính:

a) $A = \sqrt 3 \left( {\sqrt {12}  - \sqrt {27}  + 5} \right) - \sqrt {75}$                                          b) $B = 2\sqrt {45}  + \sqrt {{{\left( {1 - \sqrt 5 } \right)}^2}}  - \frac{8}{{\sqrt 5  + 1}}$

Bài 2 (2 điểm):

Giải các phương trình sau:

a) $\frac{1}{2}\sqrt {x - 2}  - \sqrt {4x - 8}  + \sqrt {9x - 18}  - 5 = 0$                                 b) $\sqrt {{x^2} - 4x + 4}  = 2x - 1$

Bài 3 (2 điểm):

Cho hai biểu thức $A = \frac{{\sqrt x }}{{\sqrt x  - 2}}$ và $B = \frac{{2\sqrt x }}{{\sqrt x  - 3}} - \frac{{x + 9\sqrt x }}{{x - 9}}$ với $x > 0,\,\,x \ne 4,\,\,x \ne 9.$

a) Tính giá trị của biểu thức $A$ khi $x = 100.$

b) Rút gọn biểu thức $B.$

c) Tìm giá trị nguyên của $x$ để biểu thức $M = A:B$ có giá trị nguyên.

Bài 4 (4 điểm):

Cho $\Delta ABC$ vuông tại $A\,\,\left( {AB < AC} \right),$ đường cao $AH,$ trung tuyến $AM.$ Gọi $D,\,\,E$ thứ tự là hình chiếu của $H$ trên $AB,\,\,AC;$ $K$ là giao điểm của $AM$ và $DE.$

a) Chứng minh $AD.AB = AE.AC.$

b) Chứng minh $AM \bot DE$ và $A{H^3} = DK.A{B^2}.$

c) Biết $HB = 3cm,\,\,HC = 7cm.$ Tính $AB,\,\,AC,\,\,DE$ và $\sqrt[3]{{B{D^2}}} + \sqrt[3]{{C{E^2}}}.$

Đề 5

Bài 1 (1,5 điểm):

1) Tính giá trị biểu thức $P = \sqrt {125}  + \sqrt {20}  - \sqrt {180}$.

2) Tìm giá trị $x$ thực biết: $\sqrt {x - 1}  + \sqrt {9x - 9}  - \sqrt {4x - 4}  = 4$.

Bài 2 (2 điểm): Rút gọn các biểu thức

1) $A = \frac{1}{{2 - \sqrt 3 }} + \frac{1}{{2 + \sqrt 3 }}$               2) $B = \sqrt {5 + 2\sqrt {{{\left( {1 - \sqrt 2 } \right)}^2}} }$                       3) $C = \frac{{x + \sqrt x  - 2}}{{\sqrt x  + 2}}$ (với $x \ge 0$)

Bài 3 (3 điểm):

Cho các biểu thức: $A = \frac{{x - 4}}{{\sqrt x  - 2}}$  và  $B = \frac{2}{{\sqrt x  - 2}} + \frac{3}{{\sqrt x  + 2}} - \frac{{x - 5\sqrt x  + 2}}{{4 - x}}$ với $x \ge 0;x \ne 4$

1) Tính giá trị của $A$ khi $x = 49$.

2) Rút gọn $B$.

3) Với $x > 4$, tìm giá trị nhỏ nhất của biểu thức $P = A.B$.

Bài 4 (3 điểm):

Cho $\Delta ABC$ vuông tại $A,$ đường cao $AH,\,\,AB = 3\,cm,\,\,BC = 6\,cm.$ Gọi $E,\,\,F$ lần lượt là hình chiếu vuông góc của $H$ trên $AB$ và $AC.$

a) Giải $\Delta ABC.$

b) Tính $AH$ và chứng minh $EF = AH.$

c) Tính $EA.EB + AF.FC.$

Bài 5 (0,5 điểm): Tìm giá trị nhỏ nhất của biểu thức $A = \frac{1}{{{x^2} + {y^2}}} + \frac{2}{{xy}} + 4xy$ với $x > 0;y > 0;x + y \le 1$.

Đề 6

Phần trắc nghiệm ( 1 điểm)

Câu 1. Căn bậc hai của 9 là:

A. 3	B. $\pm 3$
C. -3	D. $\pm 81$

Câu 2. $\sqrt {3 - 5x}$ xác định khi và chỉ khi

A. $x > \frac{3}{5}$ .	B. $x < \frac{3}{5}$ .
C. $x \le \frac{3}{5}$ .	D. $x \ge \frac{3}{5}$ .

Câu 3 . Một cái thang dài $3,5\,{\rm{m}}$ đặt dựa vào tường, góc “an toàn” giữa thang và mặt đất để thang không đổ khi người trèo lên là $65^\circ$ . Khoảng cách “an toàn” từ chân tường đến chân thang (Kết quả làm tròn đến chữ số thập phân thứ nhất) là:

A. 1,4 m.	B. 1,48 m.
C. 1 m.	D. 1,5 m.

Câu 4 . Tam giác $ABC$ vuông tại $A$ , có đường cao $AH$ chia cạnh huyền thành hai đoạn thẳng có độ dài $3,6\,{\rm{cm}}$ và $6,4\,{\rm{cm}}$ . Độ dài một trong các cạnh góc vuông là

A. 8 cm.	B. 4,8 cm.
C. 64 cm.	D. 10 cm.

Phần tự luận (9 điểm)

Bài 1 (1,5 điểm ) Thực hiện phép tính.

a) $\sqrt {20}  + 2\sqrt {45}  - 15\sqrt {\frac{1}{5}}$ .

b)$\frac{{\sqrt {35}  - \sqrt 7 }}{{\sqrt 5  - 1}} + \frac{{12}}{{\sqrt 7  - 1}}$ .

c)$\sqrt {8 + 2\sqrt 7 }  - \sqrt {28}$ .

Bài 2 (2 điểm ) Giải các phương trình sau:

Bài 3 ( 2 điểm ) Cho biểu thức $M = \frac{{\sqrt x  - 1}}{{\sqrt x }}$ và $P = \frac{{\sqrt x  - 2}}{{\sqrt x  + 1}} + \frac{{2 + 8\sqrt x }}{{x - 1}} - \frac{2}{{1 - \sqrt x }}$ với $x > 0;\,\,x \ne 1;x \ne 5$

a) Tính giá trị của $M$ khi $x = 9$ .

b) Chứng minh $P = \frac{{\sqrt x  + 6}}{{\sqrt x  - 1}}$ .

c) Đặt $Q = M.P + \frac{{x - 5}}{{\sqrt x }}$ . Hãy so sánh $Q$ với 3.

Bài 4 (3,5 điểm): Cho tam giác $ABC$ nhọn , đường cao $AK$ .

a) Giải tam giác $ACK$ biết $\widehat C = 30^\circ ,\,AK = 3\,{\rm{cm}}$ .

b) Chứng minh $AK = \frac{{BC}}{{\cot B + \cot C}}$ .

c) Biết $BC = 5\,{\rm{cm}},\widehat B = 68^\circ ,\widehat C = 30^\circ$ . Tính diện tích tam giác $ABC$ ( kết quả làm tròn chữ số thập phân thứ nhất).

d) Vẽ hình chữ nhật $CKAD$ , $DB$ cắt $AK$ tại $N$ . Chứng minh rằng $\frac{1}{{A{K^2}}} = \frac{{{{\cot }^2}\widehat {ACB}}}{{D{N^2}}} + \frac{1}{{D{B^2}}}$ .

-------- Hết --------

Đề 7

Bài 1 (2,5 điểm) Cho hai biểu thức

$A = \frac{{x + 2\sqrt x + 5}}{{\sqrt x - 3}}$ và $B = \frac{{2\sqrt x - 9}}{{x - 5\sqrt x + 6}} - \frac{{\sqrt x + 3}}{{\sqrt x - 2}} - \frac{{2\sqrt x + 1}}{{3 - \sqrt x }}$ với $\left( {x \ge 0,x \ne 4,x \ne 9} \right)$

a) Tính giá trị của A khi $x = 16.$

b) Rút gọn biểu thức $B$

c) Biết rằng $P = A:B$ . Tìm giá trị nhỏ nhất của $P$

Bài 2 (3,0 điểm) Giải các phương trình sau:

a) $\sqrt {x - 5} = 2$

b) $\sqrt {{x^2} - 6x + 9} = 5$

c) $\sqrt {4{x^2} - 4x + 1} = x + 1$

d) $\sqrt {{x^2} - 4x + 4} = \sqrt {4{x^2} - 12x + 9}$

Bài 3 ( 3,5 điểm) Cho tam giác $ABC$ vuông tại $A$ ( $AB > AC$ ), đường cao $AH$ ( $H \in BC$ ). Vẽ phân giác $AD$ của góc $BAH$ ( $D \in BH$ ). Cho $M$ là trung điểm của $BA$ .

a) Cho $AC = 3cm$ ; $AB = 4cm$ . Hãy giải tam giác $ABC$ ?(Làm tròn đến độ)

b) Tính diện tích tam giác $AHC$

c) Chứng minh rằng: $\frac{{DH}}{{DB}} = \frac{{HC}}{{AC}}$

d) Gọi $E$ là giao điểm của $DM$ và $AH$ . Chứng minh: ${S_{\Delta A{\rm{E}}C}} = {S_{\Delta DEC}}$

Bài 4 (1,0 điểm)

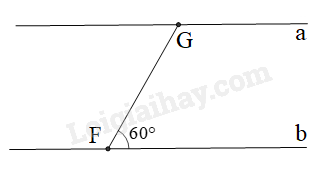
Một con thuyền ở địa điểm $F$ di chuyển từ bờ sông $b$ sang bờ sông $a$ với vận tốc trung bình là $6$ km/h, vượt qua khúc sông nước chảy mạnh trong $5$ phút. Biết đường đi của con thuyền là $FG$ , tạo với bờ sông một góc $60^\circ$ .

a) Tính $FG$

b) Tính chiều rộng của khúc sông (làm tròn đến mét)

-------- Hết --------

Đề 8

Bài 1 (2 điểm) Thực hiện phép tính

a) $A = 3\sqrt {125} + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}}$

b) $B = \left( {2 + \sqrt 7 } \right)\sqrt {11 - 4\sqrt 7 } - \frac{{\sqrt {20} + 5}}{{\sqrt 5 + 2}}$

c) $C = {\sin ^2}{25^0} + {\sin ^2}{65^0} - \tan {35^0} + \cot {55^0} - \frac{{\cot {{32}^0}}}{{\tan {{58}^0}}}$

Bài 2 ( 1,5 điểm) Giải các phương trình sau:

a) $\sqrt {9x - 27} - \sqrt {x - 3} = 6$.

b) $\sqrt {{x^2} + 2x + 1} - \sqrt {x + 1} = 0$.

Bài 3 (2 ,5 điểm) Cho hai biểu thức $A = \frac{{\sqrt x - 2}}{{x + \sqrt x + 1}}$ và $B = \frac{{2\sqrt x }}{{\sqrt x - 2}} - \frac{{5\sqrt x - 2}}{{x - 2\sqrt x }} - \frac{{\sqrt x + 1}}{{\sqrt x }}$ với $x > 0;\,x \ne 4$

1) Tính giá trị biểu thức $A$ khi $x = 9$ .

2) Rút gọn biểu thức $B$ .

3) Tìm các giá trị của $x$ để $B \le - \frac{1}{2}$ .

4) Tìm giá trị lớn nhất của biểu thức $M = \frac{{6A}}{B}$ .

Bài 4 (3,5 điểm)

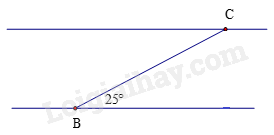
1) Một con thuyền đi qua một khúc sông theo hướng từ $B$ đến $C$ (như hình vẽ) với vận tốc $3,5km/h$ trong $12$ phút. Biết rằng đường đi của thuyền tạo với bờ sông một góc $25^\circ$ . Hãy tính chiều rộng của khúc sông ? (Kết quả tính theo đơn vị $km$ ,làm tròn kết quả đến chữ số thập phân thứ hai).

2) Cho tam giác $ABC$ nhọn có đường cao $AH$ . Gọi $E$ là hình chiếu của $H$ trên $AB$ .

a. Biết $AE = 3,6cm$ ; $BE = 6,4cm$ . Tính $AH,EH$ và góc $B.$ (Số đo góc làm tròn đến độ)

b. Kẻ $HF$ vuông góc với $AC$ tại $F.$ Chứng minh $AB.AE = AC.AF.$

c. Đường thẳng qua $A$ và vuông góc với $EF$ cắt $BC$ tại $D$ ; $EF$ cắt $AH$ tại $O.$ Chứng minh rằng ${S_{ADC}} = \frac{{{S_{AOE}}}}{{{{\sin }^2}B.{{\sin }^2}C}}$

Bài 5 (0,5 điểm) Giải phương trình $2\sqrt {2x - 1} = 8 - \sqrt[3]{{x + 3}}$ .

-------- Hết --------

Đề 9

Bài 1 ( 2,5 điểm)

Cho hai biểu thức $A = \frac{{\sqrt x + 1}}{{\sqrt x - 3}}$ và $B = \frac{{x - 3}}{{x - 9}} + \frac{1}{{\sqrt x + 3}} - \frac{2}{{3 - \sqrt x }}$ với $x \ge 0$ ; $x \ne 9$ .

a) Tính giá trị của biểu thức $A$ với $x = 0,25$ .

b) Rút gọn biểu thức $B$ .

c) Cho $P = \frac{B}{A}$ . Chứng minh rằng $P < 1$ với mọi giá trị $x$ thỏa mãn điều kiện.

Bài 2 (2,0 điểm) Tìm $x$ , biết

a) $\sqrt {25x + 75} + 15.\sqrt {\frac{{x + 3}}{{25}}} = 2 + 4\sqrt {x + 3}$

b) $\sqrt {{x^2} - 2x + 1} = 2x + 3$

Bài 3 (1,5 điểm)

Một chiếc thang dài $3,5$ m. Cần đặt chân thang cách tường một khoảng bằng bao nhiêu để nó tạo với phương nằm ngang của mặt đất một góc an toàn $65^\circ$ . (làm tròn kết quả đến chữ số thập phân thứ hai)

Bài 4 (3,5 điểm)

Cho đường tròn $(O;R)$ , đường kính $AB$ . Kẻ tiếp tuyến $Ax$ , lấy điểm $C$ trên $Ax(AC > R)$ . Từ $C$ kẻ tiếp tuyến tại $CD$ với $(O)$ $(D$ là tiếp điểm $)$ .

a) Chứng minh bốn điểm $A\,,C,D,O$ cùng thuộc một đường tròn.

b) Chứng minh $OC{\mkern 1mu} {\rm{//}}{\mkern 1mu} BD$ .

c) Đường thẳng vuông góc với $A\,B$ tại $O$ cắt tia $BD$ tại $M$ . Chứng minh $OMCD$ là hình bình hành.

d) Gọi $K$ là giao điểm của $CD$ và $OM$ , $E$ là giao điểm của $CD$ và $OD$ ; $I$ là giao điểm của $AM$ và $OC$ . Chứng minh $E$ , $K$ , $I$ thẳng hàng.

Bài 5 (0,5 điểm) Cho $x$ , $y$ , $z$ là các số thực không âm thỏa mãn $x + y + z = 1$ . Tính giá trị biểu thức $P = \sqrt {2{x^2} + x + 1} + \sqrt {2{y^2} + y + 1} + \sqrt {2{z^2} + z + 1}$

-------- Hết --------

Đề 10

Bài 1 (2 điểm) Tính.

a) $2\sqrt 9 + 6\sqrt 4 - 3\sqrt {25}$ .

b) $\sqrt {{{\left( {\sqrt 3 - \sqrt 2 } \right)}^2}} - \sqrt {{{\left( {\sqrt 3 + \sqrt 2 } \right)}^2}}$ .

c) $\frac{{5 + \sqrt 5 }}{{\sqrt 5 }} + \frac{{3 + \sqrt 3 }}{{\sqrt 3 + 1}} - \left( {\sqrt 3 + \sqrt 5 } \right)$.

d) $\frac{2}{{\sqrt 3 + 1}} - \frac{1}{{\sqrt 3 - 2}} + \frac{6}{{\sqrt 3 + 3}}$ .

Bài 2 (2,0 điểm) Giải phương trình

a) $\frac{1}{3}\sqrt {9x + 9} - 2\sqrt {x + 1} + 8\sqrt {\frac{{4x + 4}}{{25}}} = 11$

b) $\sqrt {x - 1} = 3 - x$

Bài 3 ( 2 điểm) Cho hai biểu thức $A = \frac{{\sqrt x - 3}}{{x - \sqrt x + 1}}$ và $B = \left( {\frac{{3\sqrt x + 6}}{{x - 9}} - \frac{2}{{\sqrt x - 3}}} \right):\frac{1}{{\sqrt x + 3}}$

(với $x \ge 0$ ; $x \ne 9$ ).

a) Tính giá trị biểu thức $A$ khi $x = 4$ .

b) Rút gọn biểu thức $B$ .

c) Cho biểu thức $P = A.B$ . Chứng minh $\left| P \right| = P$ với $x \ge 0$ ; $x \ne 9$ .

Bài 4 (3,5 điểm) (Kết quả làm tròn đến số thập phân thứ hai và số đo góc làm tròn đến độ) .

1) Một máy bay bay với vận tốc 5m/s lên cao theo phương tạo với đường băng một góc $40^\circ$ . Hỏi sau $6$ phút máy bay ở độ cao bao nhiêu so với đường băng.

2) Cho tam giác $ABC$ vuông tại $A$ , kẻ $AH$ vuông góc với $BC$ tại $H$ , biết $BH = 3,6$ cm; $CH = 6,4$ cm.

a) Hãy tính độ dài các đoạn thẳng $AH,\,AB$ và tính số đo $HCA$

b) Gọi $M$ và $N$ lần lượt là hình chiếu của $H$ lên $AB$ và $AC$ . Chứng minh tam giác $AMN$ đồng dạng với tam giác $ACB$ .

c) Tính diện tích tứ giác $BMNC$

Bài 5 (0,5 điểm) Giải phương trình $\sqrt[3]{{x - 2}} + \sqrt {x + 1} = 3$

-------- Hết --------

Đề 11

Câu 1: Tính

a) $\sqrt {50}  + \sqrt {32}  - 3\sqrt {18}  + 4\sqrt 8$

b) $\frac{{5 - 2\sqrt 5 }}{{\sqrt 5  - 2}} - \sqrt {6 - 2\sqrt 5 }$

Câu 2: Giải phương trình

a) $\sqrt {4{x^2} - 4x + 1}  = 5$

b) $3\sqrt {x - 2}  - \sqrt {4x - 8}  + 4\sqrt {\frac{{9x - 18}}{4}}  = 14$

c) $\sqrt[3]{{4x - 1}} = 3$

Câu 3: Cho hai biểu thức $A = \frac{{\sqrt x {\rm{ \;}} + 2}}{{\sqrt x {\rm{ \;}} - 2}}$ và $B = \frac{3}{{\sqrt x {\rm{ \;}} + 2}} - \frac{{\sqrt x {\rm{ \;}} + 10}}{{x - 4}}$ (với $x \ge 0,x \ne 4$)

a) Tính giá trị của A khi x = 9.

b) Rút gọn biểu thức B.

c) Cho biểu thức P =  A.B. Tìm tất cả các giá trị của x để $P \le {\rm{ \;}} - 1$.

Câu 4: Hãy tính chiều cao của tháp Eiffel mà không cần lên tận đỉnh tháp khi biết góc tạo bởi tia nắng mặt trời với mặt đất là ${62^0}$ và bóng của tháp trên mặt đất khi đó là 172m (làm tròn kết quả tới chữ số thập phân thứ nhất)

Câu 5: Cho tam giác ABC vuông tại A, có AB = 12cm, AC = 16cm. Kẻ đường cao AM. Kẻ $ME \bot AB.$

a) Tính $BC,{\mkern 1mu} {\mkern 1mu} \widehat B,{\mkern 1mu} {\mkern 1mu} \widehat C.$

b) Tính độ dài $AM,{\mkern 1mu} {\mkern 1mu} BM.$

c) Chứng minh $AE.AB = A{C^2} - M{C^2}.$

Câu 6 : Chứng minh rằng nếu $xyz = 1$ thì $\frac{1}{{1 + x + xy}} + \frac{1}{{1 + y + yz}} + \frac{1}{{1 + z + zx}} = 1$.

-------- Hết --------

Đề 12

Câu 1: Thực hiện phép tính:

a) $4\sqrt 5  - 3\sqrt {20}  + \sqrt {45}$

b) $\sqrt {{{(\sqrt 3  - 1)}^2}}  + \frac{6}{{\sqrt 3 }} - 15\sqrt {\frac{1}{3}}  + 1$

Câu 2: Giải phương trình:

a) $\sqrt {x - 3}  + \sqrt {9x - 27}  - \frac{1}{2}\sqrt {4x - 12}  = 6$

b) $\sqrt {{x^2} - 2x + 1}  + 2 = 5$

Câu 3: Cho hai biểu thức $A = \frac{{3\sqrt x }}{{\sqrt x {\rm{ \;}} + 2}}$ và $B = \frac{{x + 4}}{{x - 4}} - \frac{2}{{\sqrt x {\rm{ \;}} - 2}}$ với $x \ge 0,x \ne 4$.

1) Tính giá trị của biểu thức A khi x = 9.

2) Chứng minh $B = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} + 2}}$.

3) Tìm số nguyên dương x lớn nhất thỏa mãn $A - B < \frac{3}{2}$.

Câu 4 : Một tòa tháp có bóng trên mất đất dài 15m, biết rằng góc tạo bởi tia nằng mặt trời với mặt đất là ${55^0}$ (minh họa như hình vẽ bên dưới). Chiều cao của tòa tháp (làm tròn đến chữ số thập phân thức hai) bằng bao nhiêu?

Câu 5: Cho $\Delta EMF$ vuông tại M có đường cao MI. Vẽ $IP \bot ME{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {P \in ME} \right),$ $IQ \bot MF{\mkern 1mu} {\mkern 1mu} \left( {Q \in MF} \right).$

a) Cho biết $ME = 4{\mkern 1mu} cm,{\mkern 1mu} {\mkern 1mu} \sin \widehat {MFE} = \frac{3}{4}.$ Tính độ dài các đoạn $EF,{\mkern 1mu} {\mkern 1mu} EI,{\mkern 1mu} {\mkern 1mu} MI.$

b) Chứng minh $MP.PE + MQ.QF = M{I^2}.$

Câu 6: Cho 4 số thực dương a, b, c, d chứng mình rằng trong 4 số ${a^2} + \frac{1}{b} + \frac{1}{c};$ ${b^2} + \frac{1}{c} + \frac{1}{d};$${c^2} + \frac{1}{d} + \frac{1}{a};{d^2} + \frac{1}{a} + \frac{1}{b}$tồn tại ít nhất 1 số không nhỏ hơn 3.

-------- Hết --------

Đề 13

Phần I: Trắc nghiệm (3 điểm).

Câu 1: Giá trị của biểu thức $P = \sqrt 5  \cdot \sqrt {20}$ là

A. 10 .

B. 5 .

C. 6 .

D. 8 .

Câu 2: Nghiệm của phương trình $\sqrt x  - 1 = 3$ là

A. 8 .

B. 9 .

C. 16 .

D. 11 .

Câu 3: Rút gọn biểu thức $\frac{2}{{\sqrt 3  - 1}} - \frac{2}{{\sqrt 3  + 1}}$ thu được kết quả là

A. 0 .

B. 2 .

C. $2\sqrt 3$.

D. $- 2\sqrt 3$.

Câu 4: Điều kiện xác định của $\sqrt {2022 - 2023x}$ là

A. $x \ge \frac{{2022}}{{2023}}$.

B. $x \le \frac{{2022}}{{2023}}$.

C. $x \ge \frac{{2023}}{{2022}}$.

D. $x \le \frac{{2023}}{{2022}}$.

Câu 5: Cho $\Delta ABC$ vuông tại ${\rm{A}}$ có $AB = 6\;{\rm{cm}},AC = 8\;{\rm{cm}}$. Độ dài đường cao ${\rm{AH}}$ bằng

A. $\frac{5}{{24}}\;{\rm{cm}}$.

B. $4,8\;{\rm{cm}}$.

C. $23,04\;{\rm{cm}}$.

D. $10\;{\rm{cm}}$.

Câu 6: Cho $\Delta ABC$ vuông tại ${\rm{A}}$, có $AB = 3,AC = 4$. Khi đó tanB bằng

A. $\frac{3}{4}$.

B. $\frac{3}{5}$.

C. $\frac{4}{3}$.

D. $\frac{4}{5}$.

Phần II. Tự luận (7 điểm):

Câu 7: (1,5d) Thực hiện phép tính:

a) $(3\sqrt 5  - 2\sqrt 3 ) \cdot \sqrt 5  + \sqrt {60}$.

b) $\sqrt {125}  - 4\sqrt {45}  + 3\sqrt {20}  + \sqrt {80}$.

Câu 8: (1,5đ) Giải phương trình:

a) $\sqrt {4x + 20}  + \sqrt {x + 5}  - \frac{1}{3}\sqrt {9x + 45}  = 4$;

b) $\frac{{2\sqrt x  - 7}}{3} + \sqrt x  - \frac{{3\sqrt x  - 5}}{2} = 1$

Câu 9: (2đ) Cho biểu thức $A = \frac{{{a^2} + \sqrt a }}{{a - \sqrt a  + 1}} - \frac{{2a + \sqrt a }}{{\sqrt a }} + 1$ với ${\rm{a}} > 0$,

a) Rút gọn biểu thức ${\rm{A}}$.

b) Tìm ${\rm{a}}$ để ${\rm{A}} = 2$.

c) Tìm a để ${\rm{A}}$ đạt giá trị nhỏ nhất.

Câu 10: (2đ) Cho $\Delta ABC$ vuông tại A có $\widehat B = {30^0},AB = 6\;{\rm{cm}}$.

a) Giải $\Delta ABC$.

b) Vẽ đường cao ${\rm{AH}}$ và trung tuyến ${\rm{AM}}$ của $\Delta ABC$. Tính diện tích $\Delta AHM$.

-------- Hết --------

Đề 14

Phần I: Trắc nghiệm

Câu 1: Kết quả của phép tính $\frac{{\sqrt 3  - 3}}{{\sqrt 3  - 1}} + 2\sqrt 3$ bằng:

A. $- 3\sqrt 3$.

B. $\sqrt 3$.

C. $3\sqrt 3$.

D. $- \sqrt 3$.

Câu 2: Căn bậc hai số học của 4 là:

A. 2

B. 2 và -2

C. 16

D. 16 và -16

Câu 3: Các căn bậc hai của $\sqrt {16}$ là:

A. – 4

B. 4

C. -4

D. - 2

Câu 4: Căn bậc ba của (-27) là:

A. 3

B. -3

C. 3 và -3

D. 9 và -9

Câu 5: Với $\sqrt {16x}  - \sqrt {25x}  =  - 3$ khi đó ${\rm{x}}$ bằng:

A. 3

B. 0

C. -9

D. 9

Câu 6: Điều kiện xác định của căn thức : $\sqrt {6 + 2x}$ là:

A. $x \le 3$

B. $x \ge 0$

C. $x \ge  - 3$

D. $x \le 6$

Câu 7: Với ${\rm{x}} > 0$ biểu thức $\sqrt {{{(3 - 2x)}^2}}$ bằng

A. $3 - 2x$.

B. $2{\rm{x}} - 3$.

C. $3 - 2{\rm{x}}$ hoăc $2{\rm{x}} - 3$.

D. $3 - 2{\rm{x}}$ và $2{\rm{x}} - 3$

Câu 8: Phép tính nào có kết quả đúng:

A. $\sqrt {100}  =  \pm 10$

B. $\sqrt 1  + \sqrt 2  = \sqrt 3$

C. $\sqrt 9  - \sqrt 4  = \sqrt 5$

D. $\sqrt {10} :\sqrt 2  = \sqrt 5$

Câu 9: Biểu thức $\sqrt {{{(3 - \sqrt 5 )}^2}}$ sau khi bỏ dấu căn là:

A. $3 - \sqrt 5$

B. $\sqrt 5  + 3$

C. $2\sqrt 5$

D. $\sqrt 5  - 3$

Câu 10: Kết quả so sánh 3 và $\sqrt {10}$ là:

A. $3 \le \sqrt {10}$

B. $3 < \sqrt {10}$

C. $3 \ge \sqrt {10}$

D. $3 > \sqrt {10}$

Câu 11: Rút gọn biểu thức $\frac{1}{{\sqrt 2  - 1}}$ là:

A. $\sqrt 2  + 1$

B. $\sqrt 2  - 1$

C. $- \sqrt 2$

D. $\sqrt 2$

Câu 12. Tam giác MNP vuông tại $M$, khẳng định nào sau đây là đúng ?

A. $MP = NP.\sin N$.

B. $MP = NP.\sin P$.

C. $MP = NP.\cos N$.

D. $MP = MN.\cot N$.

Câu 13: Một cột điện cao $5\;{\rm{m}}$ có bóng trên mặt đất dài $4\;{\rm{m}}$. Khi đó phương tia nắng tạo với mặt đất một góc xấp xi bằng (làm tròn đến phút)

A. ${38^\circ }{40^\prime }$.

B. ${53^0}{8^\prime }$.

C. ${36^\circ }{52^\prime }$.

D. ${51^0}{20^\prime }$.

Câu 14: Cho tam giác ${\rm{ABC}}$ vuông tại ${\rm{A}}$ có đường cao ${\rm{AH}},{\mathop{\rm Sin}\nolimits} {\rm{B}}$ bằng

A. $\frac{{AH}}{{AC}}$

B. $\frac{{AH}}{{AB}}$

C. $\frac{{AB}}{{BC}}$

D. $\frac{{AH}}{{BC}}$

Câu 15. Cho tam giác ${\rm{ABC}}$ vuông tại ${\rm{A}}$ có ${\rm{AB}} = 6\;{\rm{cm}};{\rm{AC}} = 8\;{\rm{cm}}$. Khi đó AH bằng

A. $7\;{\rm{cm}}$

B. $3,5\;{\rm{cm}}$

C. $4,8\;{\rm{cm}}$

D. $5,2\;{\rm{cm}}$

Phần II. Tự luận

Câu 1:

a) Thưc hię̂n phép tính và thu gọn các biểu thức sau:

$A = (3\sqrt {18}  + \sqrt 6  - 2\sqrt {32} )\sqrt 2  - 2\sqrt 3$

$B = \left( {\frac{4}{{1 - \sqrt 5 }} + \frac{1}{{2 + \sqrt 5 }} - \frac{4}{{3 - \sqrt 5 }}} \right) \cdot (\sqrt 5  - 6)$

b) Giải phương trình $\sqrt {9x - 45}  - 14\sqrt {\frac{{x - 5}}{{49}}}  + \frac{1}{4}\sqrt {4x - 20}  = 3$

Câu 2: Với $x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 9$. Cho hai biểu thức $A = \frac{{2\sqrt x {\rm{ \;}} - 2}}{{\sqrt x {\rm{ \;}} - 3}}$ và $B = \frac{{2\sqrt x }}{{\sqrt x {\rm{ \;}} + 3}} + \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 3}} - \frac{{3x + 3}}{{x - 9}}$.

1. Tính giá trị của biểu thức A khi $x = 49$.

2. Rút gọn biểu thức B.

3. Tìm $x$ để $\frac{B}{{A - 1}} < \frac{{ - 1}}{3}$.

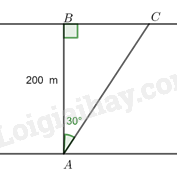
Câu 3: Một khúc sông rộng 200m. Một chiếc xuồng máy dự định chèo vuông góc với bờ sông để sang bờ bên kia (từ A đến B) nhưng bị dòng nước đẩy xiên đi một góc 30 độ (đến C). Hỏi chiếc xuồng máy đã phải đi một quãng đường dài hơn so với dự định là bao nhiêu mét (làm tròn đến hàng đơn vị).

Câu 4: Cho hình vuông ABCD và điểm E nằm trên cạnh BC biết $AB = 4cm$, $BE = \frac{3}{4}BC$. Tia Ax vuông góc với AE tại A cắt tia CD tại F.

a) Tính diện tích tam giác AEF.

b) Gọi I là trung điểm của đoạn thẳng EF, tia AI cắt cạnh CD tại K. Chứng minh $A{E^2} = KF.CF$.

Câu 5: ( 0,5 điểm) Cho x là số thực dương. Tìm giá trị nhỏ nhất của biểu thức sau: $M = {x^2} + \frac{9}{x} - 5x + 2011.$

-------- Hết --------

Đề 15

Câu 1: Rút gọn các biểu thức sau:

a) $A = \sqrt {{{(3 - \sqrt 5 )}^2}}  + \frac{3}{4}\sqrt {80}  - 6$

b) $B = \frac{{\sqrt {18} }}{{\sqrt 6 }} + \frac{4}{{\sqrt 5  - 1}} - \frac{{3 + \sqrt 3 }}{{1 + \sqrt 3 }}$

c) $C = {\sin ^2}{33^0} - \frac{{\tan {{29}^0}}}{{\cot {{61}^0}}} - \frac{1}{2} \cdot {\cos ^2}{60^0} + {\sin ^2}{57^0}$

Câu 2: Giải các phương trình sau:

a) $9\sqrt {x + 2}  - \frac{1}{3}\sqrt {9x + 18}  = 24$

b) $\sqrt {{x^2} - 6x + 9}  - 2\sqrt {x - 3}  = 0$

Câu 3: Cho biểu thức $P = \left( {\frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 1}} - \frac{1}{{x - \sqrt x }}} \right):\left( {\frac{1}{{\sqrt x {\rm{ \;}} + 1}} + \frac{2}{{x - 1}}} \right)$.

a) Rút gọn $P$

b) Tính giá trị của $P$ biết $x = 7 - 4\sqrt 3$

c) Tìm $x$ biết $P = \frac{3}{2}$

Câu 4:

1) Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 6cm và diện tích tam giác ABC bằng $24c{m^2}$. Tính độ dài các đoạn thẳng AC,BC,AH.

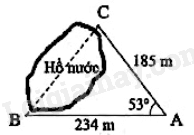
2) Tính khoảng cách giữa hai điểm B và C, biết rằng từ vị trị A ta đo được $AB = 234{\mkern 1mu} m,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} AC = 185{\mkern 1mu} m$ và $\widehat {BAC} = {53^0}$ (kết quả tính bằng mét và làm tròn đến hàng đơn vị).

3) Cho tam giác ABC vuông tại $A{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {AB < AC} \right)$ với đường cao AH. Goi D và E lần lượt là hình chiếu của H trên AB và AC. Chứng minh:

a) $AB.AD = AC.AE$

b) $\frac{{A{B^2}}}{{A{C^2}}} = \frac{{BH}}{{CH}}$

Câu 5: Cho các số thực $x,y > 0$ thỏa mãn $\sqrt x  + \sqrt y  = 2$. Tìm giá trị nhỏ nhất của biều thức:

$P = x + y - 2022\sqrt {xy}$

-------- Hết --------