Bài 10 trang 76 SGK Toán 9 tập 1
Vẽ một tam giác vuông...
Đề bài
Vẽ một tam giác vuông có một góc nhọn \(34^{\circ}\) rồi viết các tỉ số lượng giác của góc \(34^{\circ}\).
Phương pháp giải - Xem chi tiết
+) Vẽ tam giác thỏa mãn yêu cầu đề bài.
+) Áp dụng công thức tính tỉ số lượng giác của một góc nhọn:
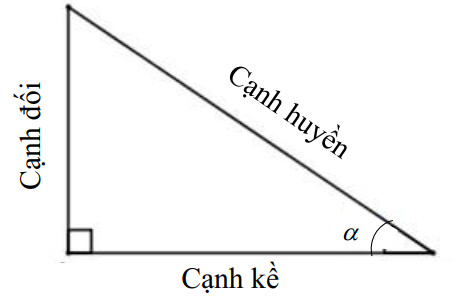
\(\sin \alpha =\dfrac{cạnh\ đối}{cạnh\ huyền};\) \(\cos \alpha = \dfrac{cạnh\ kề}{cạnh\ huyền}\);
\(\tan \alpha = \dfrac{cạnh\ đối}{cạnh\ kề};\) \(\cot \alpha =\dfrac{cạnh\ kề}{cạnh\ đối}.\)
Lời giải chi tiết
Vẽ tam giác \(ABC\) vuông tại \(A\) với \(\widehat{B}=34^{\circ}\).
Để vẽ được tam giác đề yêu cầu, chúng ta thực hiện các bước như sau:
B1. Vẽ đoạn thẳng \(AB\) với độ dài bất kì.
B2. Từ \(A\) dựng tia \(Ax\) vuông góc với đoạn thẳng \(AB\)
B3. Từ \(B\) dùng thước đo góc vẽ tia \(By\) sao cho góc \(ABy\) bằng \(34\) độ.
B4. \(Ax\) và \(By\) cắt nhau tại \(C\).
B5. Nối các điểm lại với nhau ta được tam giác \(ABC\) cần dựng.
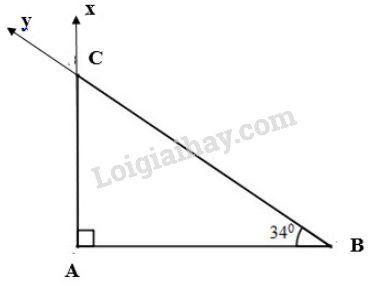
Tỉ số lượng giác của góc \(\widehat{B}=34^o\) là:
\(\sin 34^o=\sin B=\dfrac{AC}{BC}\)
\(\cos 34^o=\cos B=\dfrac{AB}{BC}\)
\(\tan 34^o=\tan B=\dfrac{AC}{AB}\)
\(\cot 34^o=\cot B=\dfrac{AB}{AC}\)