Bài 16 trang 52 SGK Toán 11 tập 2 - Chân trời sáng tạo — Không quảng cáo

Đề bài

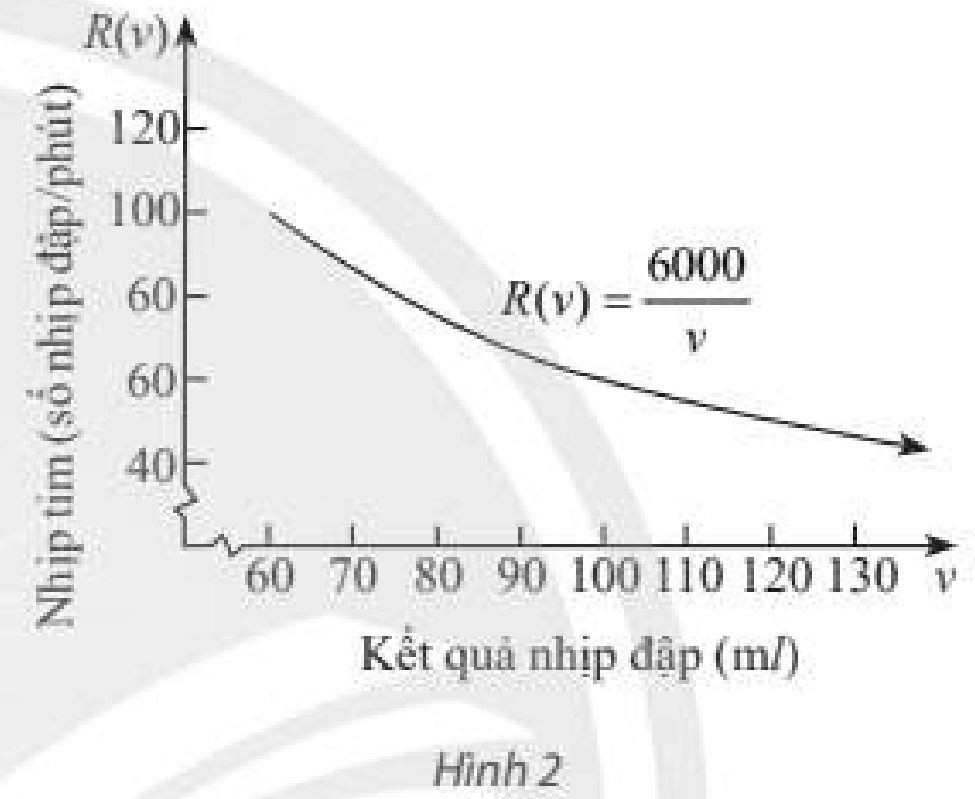
Hàm số $R\left( v \right) = \frac{{6000}}{v}$ có thể được sử dụng để xác định nhịp tim $R$ của một người mà tim của người đó có thể đây đi được $6000ml$ máu trên mỗi phút và $v{\rm{ }}ml$ máu trên mỗi nhịp đập (theo Bách khoa toàn thư Y học “Harrison's internal medicine 21st edition”). Tìm tốc độ thay đổi của nhịp tim khi lượng máu tim đẩy đi ở một nhịp là $v = 80$.

Lời giải chi tiết

Ta có: $R'\left( v \right) = 6000.\left( { - \frac{1}{{{v^2}}}} \right) =  - \frac{{6000}}{{{v^2}}}$.

Tốc độ thay đổi của nhịp tim khi lượng máu tim đẩy đi ở một nhịp là $v = 80$ là: $R'\left( {80} \right) =  - \frac{{6000}}{{{{80}^2}}} =  - 0,9375$.