Bài 17 trang 135 SGK Toán 9 tập 2
Khi quay tam giác ABC vuông ở A một vòng quanh cạnh góc vuông AC cố định, ta được một hình nón. Biết rằng BC = 4dm, góc ACB = 30o. Tính diện tích xung quanh và thể tích hình nón.
Đề bài
Khi quay tam giác \(ABC\) vuông ở \(A\) một vòng quanh cạnh góc vuông \(AC\) cố định, ta được một hình nón. Biết rằng \(BC = 4dm,\) góc \(\widehat {ACB} = {30^0}.\) Tính diện tích xung quanh và thể tích hình nón.
Phương pháp giải - Xem chi tiết
+) Diện tích xung quanh của hình nón: \(S= \pi rl.\)
+) Thể tích của hình nón: \(V=\dfrac{1}{3 } \pi r^2h.\)
Lời giải chi tiết
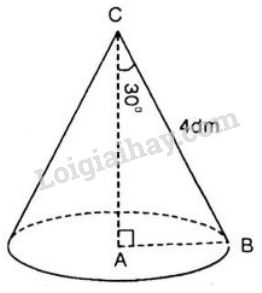
Trong tam giác vuông \(ABC\), ta có:
\(\eqalign{ & AB = BC.\sin C = BC.\sin {30^0} = 4.{1 \over 2} = 2\left( {dm} \right) \cr & AC = BC.\cos C = BC.\cos {30^0} = 4.{{\sqrt 3 } \over 2} \cr&= 2\sqrt 3 \left( {dm} \right) \cr} \)
Ta có: \(S_{xq}= πRl = π. 2. 4 = 8 π \) \((dm^2).\)
\(\displaystyle V = {1 \over 3}\pi {R^2}h = {1 \over 3}\pi {.2^2}.2\sqrt 3 = {{8\sqrt 3 .\pi } \over 3}(d{m^3}).\)