Bài 2 trang 113 SGK Toán 11 tập 1 - Cánh Diều
Cho hình hộp ABCD.A’B’C’D‘. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh BC, AA‘, C’D‘, AD‘. Chứng minh rằng:
Đề bài
Cho hình hộp ABCD.A’B’C’D‘ . Gọi M, N, P, Q lần lượt là trung điểm của các cạnh BC, AA‘, C’D‘, AD‘ . Chứng minh rằng:
a) NQ // A’D‘ và \(NQ = \frac{1}{2}A'D'\)
b) Tứ giác MNQC là hình bình hành
c) MN // (ACD‘)
d) (MNP) // (ACD‘)
Phương pháp giải - Xem chi tiết
- Hình tứ giác có các cặp cạnh song song là hình bình hành
- Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) thì a song song với (P)
- Nếu mặt phẳng (P) chứa hai đường thằng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q)
Lời giải chi tiết
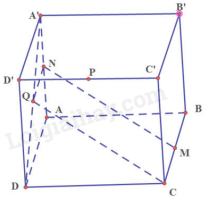
a) Ta có: N là trung điểm của AA’ nên \(\frac{{AN}}{{AA'}} = \frac{1}{2}\)
Q là trung điểm của AD’ nên \(\frac{{AQ}}{{AD'}} = \frac{1}{2}\)
Theo định lý Ta – let, ta có NQ // A’D’
Suy ra \(\frac{{NQ}}{{A'D'}} = \frac{{AN}}{{AA'}} = \frac{1}{2}\) nên\(NQ = \frac{1}{2}A'D'\)
b) Ta có: NQ // A’D’ mà A’D’ // BC nên NQ // BC hay NQ // MC (1)
Ta có \(NQ = \frac{1}{2}A'D'\) mà A’D’ = BC, \(MC = \frac{1}{2}BC\) , nên NQ = MC (2)
Từ (1) và (2) suy ra MNQC là hình bình hành
c) Ta có: MNQC là hình bình hành nên MN // CQ
Mà CQ thuộc (ACD’)
Nên MN // (ACD’)
d) Gọi O là trung điểm của AC
Tam giác ACB có: O, M là trung điểm của AC, BC
Suy ra: OM // AB nên \(OM = \frac{1}{2}AB\)
Mà AB = C’D’, \(D'P = \frac{1}{2}C'D\) ,
Suy ra OM = D’P (1)
Ta có: OM // AB, AB // C’D’ nên OM // C’D‘ hay OM // D’P (2)
Từ (1) và (2) suy ra OMPD’ là hình bình hành. Do đó: MP // OD’
Mà OD’ thuộc (ACD’)
Suy ra: MP // (ACD’)
Mà MN thuộc (ACD’)
Do đó: (MNP) // (ACD’)