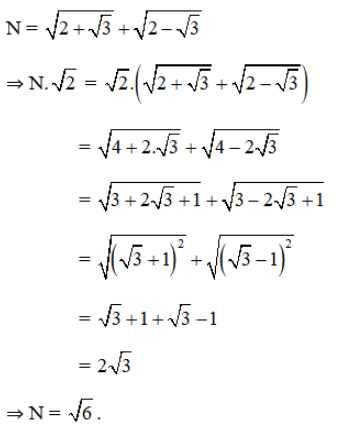Bài 2 trang 131 SGK Toán 9 tập 2
Rút gọn các biểu thức:
Đề bài
Rút gọn các biểu thức:
\(M = \sqrt {3 - 2\sqrt 2 } - \sqrt {6 + 4\sqrt 2 } \)
\(N = \sqrt {2 + \sqrt 3 } + \sqrt {2 - \sqrt 3 } \)
Phương pháp giải - Xem chi tiết
Sử dụng công thức hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\;\;khi\;\;\;A \ge 0\\- A\;\;\;khi\;\;A < 0\end{array} \right..\)
Lời giải chi tiết
\(\eqalign{&+) M = \sqrt {3 - 2\sqrt 2 } - \sqrt {6 + 4\sqrt 2 } \cr & =\sqrt {{{\left( {\sqrt 2 } \right)}^2} - 2\sqrt 2 .1 + {1^2}}- \sqrt {{{\left( 2 \right)}^2} + 2.2.\sqrt 2 + {{\left( {\sqrt 2 } \right)}^2}} \cr & = \sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} - \sqrt {{{\left( {2 + \sqrt 2 } \right)}^2}} \cr & = \left| {\sqrt 2 - 1} \right| - \left| {2 + \sqrt 2 } \right| \cr & = \sqrt 2 - 1 - 2 - \sqrt 2 = - 3 .\cr} \)
+) Cách 1:
\(\eqalign{ & N = \sqrt {2 + \sqrt 3 } + \sqrt {2 - \sqrt 3 } \cr & \Rightarrow {N^2} = {\left( {\sqrt {2 + \sqrt 3 } + \sqrt {2 - \sqrt 3 } } \right)^2} \cr & = 2 + \sqrt 3 + 2\sqrt {\left( {2 + \sqrt 3 } \right)\left( {2 - \sqrt 3 } \right)} + 2 - \sqrt 3 \cr & = 4 + 2\sqrt {4 - 3} = 6. \cr} \)
Vì \(N > 0\) nên \(N^2 = 6 ⇒ N = \sqrt6.\)
Vậy \(N = \sqrt {2 + \sqrt 3 } + \sqrt {2 - \sqrt 3 } = \sqrt 6. \)
Cách 2: