Bài 2 trang 69 SGK Toán 9 tập 2
Cho hai đường thẳng xy và st cắt nhau tại O
Đề bài
Cho hai đường thẳng \(xy\) và \(st\) cắt nhau tại \(O\), trong các góc tạo thành có góc \(40^{\circ}\). Vẽ một đường tròn tâm \(O\). Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.
Phương pháp giải - Xem chi tiết
+ Sử dụng hai góc kề bù có tổng số đo bằng \(180^\circ .\)
+ Hai góc đối đỉnh có số đo bằng nhau
Lời giải chi tiết
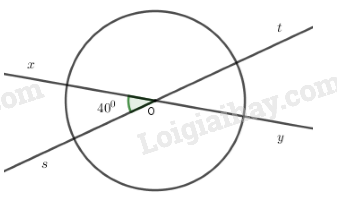
Ta có \(\widehat {xOs} = 40^\circ \) , suy ra \(\widehat {yOt} = \widehat {xOs} = 40^\circ \) (hai góc đối đỉnh)
Lại có \(\widehat {xOs} + \widehat {xOt} = 180^\circ \) (hai góc kề bù) nên \(\widehat {xOt} = 180^\circ - \widehat {xOs} = 180^\circ - 40^\circ = 140^\circ .\)
Lại có \(\widehat {sOy} = \widehat {xOt} = 140^\circ \) (hai góc đối đỉnh)
Vậy \(\widehat {xOt} = \widehat {sOy} = 140^\circ ;\,\widehat {xOs} = \widehat {tOy} = 40^\circ \)
và \(\widehat{xOy}\) = \(\widehat{sOt}\) = \(180^{\circ}\)