Bài 2 trang 7 SGK Toán 9 tập 2 — Không quảng cáo

Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:

LG a

$3x - y = 2$

Phương pháp giải:

1) Tìm nghiệm tổng quát của phương trình:

+) Nếu $a \ne 0$ thì tìm $x$ theo $y$. Khi đó công thức nghiệm là:

$\left\{ \matrix{ x = \dfrac{c - by}{a} \hfill \cr y \in \mathbb{R} \hfill \cr} \right.$

+) Nếu $b \ne 0$ thì tìm $y$ theo $x$. Khi đó công thức nghiệm là:

$\left\{ \matrix{ y = \dfrac{c - ax}{b} \hfill \cr x \in \mathbb{R} \hfill \cr} \right.$

2) Cách vẽ đường thẳng có phương trình: $ax+by=c$.

+) Nếu $a \ne 0,\ b \ne 0$ thì vẽ đường thẳng $y=\dfrac{-a}{b}x+\dfrac{c}{b}$

+) Nếu $a \ne 0,\ b=0$ thì vẽ đường thẳng $x=\dfrac{c}{a}$ song song hoặc trùng với trục tung.

+) Nếu $a =0,\ b \ne 0$ thì vẽ đường thẳng $y=\dfrac{c}{a}$ song song hoặc trùng với trục hoành.

Lời giải chi tiết:

Ta có phương trình $3x - y = 2 \Leftrightarrow y=3x -2$. Nghiệm tổng quát của phương trình là:

$\left\{\begin{matrix} x \in R & & \\ y = 3x - 2 & & \end{matrix}\right.$

* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình $y = 3x - 2$ :

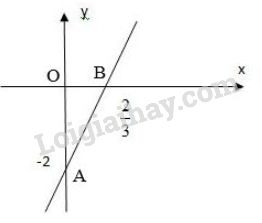
Cho $x = 0 \Rightarrow y =  - 2$ ta được $A(0; -2)$.

Cho $y = 0 \Rightarrow x = \dfrac{2}{3}$ ta được $B {\left(\dfrac{2}{3}; 0 \right)}$.

Biểu diễn cặp điểm $A(0; -2)$ và $B{\left(\dfrac{2}{3}; 0 \right)}$ trên hệ trục tọa độ và đường thẳng $AB$ chính là tập nghiệm của phương trình $3x - y = 2$.

LG b

$x + 5y = 3$

Phương pháp giải:

1) Tìm nghiệm tổng quát của phương trình:

+) Nếu $a \ne 0$ thì tìm $x$ theo $y$. Khi đó công thức nghiệm là:

$\left\{ \matrix{ x = \dfrac{c - by}{a} \hfill \cr y \in \mathbb{R} \hfill \cr} \right.$

+) Nếu $b \ne 0$ thì tìm $y$ theo $x$. Khi đó công thức nghiệm là:

$\left\{ \matrix{ y = \dfrac{c - ax}{b} \hfill \cr x \in \mathbb{R} \hfill \cr} \right.$

2) Cách vẽ đường thẳng có phuương trình: $ax+by=c$.

+) Nếu $a \ne 0,\ b \ne 0$ thì vẽ đường thẳng $y=\dfrac{-a}{b}x+\dfrac{c}{b}$

+) Nếu $a \ne 0,\ b=0$ thì vẽ đường thẳng $x=\dfrac{c}{a}$ song song hoặc trùng với trục tung.

+) Nếu $a =0,\ b \ne 0$ thì vẽ đường thẳng $y=\dfrac{c}{a}$ song song hoặc trùng với trục hoành.

Lời giải chi tiết:

Ta có phương trình $x + 5y = 3 \Leftrightarrow x=-5y+3$. Nghiệm tổng quát của phương trình là:

$\left\{\begin{matrix} x = -5y + 3 & & \\ y \in R & & \end{matrix}\right.$

* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình $x=-5y+3$ :

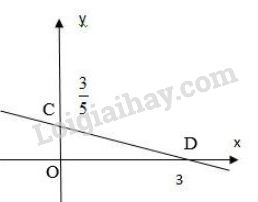
+) Cho  $x = 0 \Rightarrow y = \dfrac{3}{5}$ ta được $C {\left( 0; \dfrac{3}{5} \right)}$.

+) Cho $y = 0 \Rightarrow x = 3$ ta được $D\left( {3;0} \right)$.

Biểu diễn cặp điểm $C {\left( 0; \dfrac{3}{5} \right)}$, $D\left( {3;0} \right)$ trên hệ trục toa độ và đường thẳng $CD$ chính là tập nghiệm của phương trình.

LG c

$4x - 3y = -1$

Phương pháp giải:

1) Tìm nghiệm tổng quát của phương trình:

+) Nếu $a \ne 0$ thì tìm $x$ theo $y$. Khi đó công thức nghiệm là:

$\left\{ \matrix{ x = \dfrac{c - by}{a} \hfill \cr y \in \mathbb{R} \hfill \cr} \right.$

+) Nếu $b \ne 0$ thì tìm $y$ theo $x$. Khi đó công thức nghiệm là:

$\left\{ \matrix{ y = \dfrac{c - ax}{b} \hfill \cr x \in \mathbb{R} \hfill \cr} \right.$

2) Cách vẽ đường thẳng có phuương trình: $ax+by=c$.

+) Nếu $a \ne 0,\ b \ne 0$ thì vẽ đường thẳng $y=\dfrac{-a}{b}x+\dfrac{c}{b}$

+) Nếu $a \ne 0,\ b=0$ thì vẽ đường thẳng $x=\dfrac{c}{a}$ song song hoặc trùng với trục tung.

+) Nếu $a =0,\ b \ne 0$ thì vẽ đường thẳng $y=\dfrac{c}{a}$ song song hoặc trùng với trục hoành.

Lời giải chi tiết:

Ta có phương trình $4x - 3y = -1 \Leftrightarrow 3y=4x+1 \Leftrightarrow y=\dfrac{4}{3}x+\dfrac{1}{3}$. Nghiệm tổng quát của phương trình là:

$\left\{\begin{matrix} x \in R & & \\ y = \dfrac{4}{3}x + \dfrac{1}{3}& & \end{matrix}\right.$

* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình $4x-3y=-1$

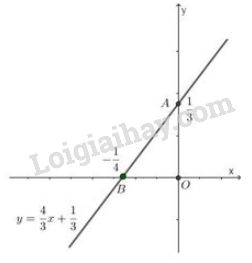
+) Cho $x = 0 \Rightarrow y = \dfrac{1}{3}$ ta được $A {\left(0;\dfrac{1}{3} \right)}$

+) Cho $y = 0 \Rightarrow x = -\dfrac{1}{4}$ ta được $B {\left(-\dfrac{1}{4};0 \right)}$

Biểu diễn cặp điểm $A {\left(0; \dfrac{1}{3} \right)}$ và $B {\left(-\dfrac{1}{4}; 0 \right)}$ trên hệ tọa độ và đường thẳng $AB$ chính là tập nghiệm của phương trình $4x-3y=-1$.

LG d

$x  +5y = 0$

Phương pháp giải:

1) Tìm nghiệm tổng quát của phương trình:

+) Nếu $a \ne 0$ thì tìm $x$ theo $y$. Khi đó công thức nghiệm là:

$\left\{ \matrix{ x = \dfrac{c - by}{a} \hfill \cr y \in \mathbb{R} \hfill \cr} \right.$

+) Nếu $b \ne 0$ thì tìm $y$ theo $x$. Khi đó công thức nghiệm là:

$\left\{ \matrix{ y = \dfrac{c - ax}{b} \hfill \cr x \in \mathbb{R} \hfill \cr} \right.$

2) Cách vẽ đường thẳng có phuương trình: $ax+by=c$.

+) Nếu $a \ne 0,\ b \ne 0$ thì vẽ đường thẳng $y=\dfrac{-a}{b}x+\dfrac{c}{b}$

+) Nếu $a \ne 0,\ b=0$ thì vẽ đường thẳng $x=\dfrac{c}{a}$ song song hoặc trùng với trục tung.

+) Nếu $a =0,\ b \ne 0$ thì vẽ đường thẳng $y=\dfrac{c}{a}$ song song hoặc trùng với trục hoành.

Lời giải chi tiết:

Ta có phương trình $x + 5y = 0 \Leftrightarrow x=-5y$. Nghiệm tổng quát của phương trình là:

$\left\{\begin{matrix} x = -5y & & \\ y \in R & & \end{matrix}\right.$

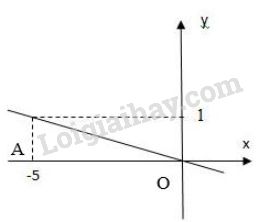
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình $x+5y=0$

+) Cho $x = 0 \Rightarrow y = 0$ ta được $O\left( {0;0} \right)$

+) Cho $y = 1 \Rightarrow x = -5$ ta được $A\left( {-5;1}\right)$.

Biểu diễn cặp điểm $O (0; 0)$ và $A (-5; 1)$ trên hệ tọa độ và đường thẳng OA chính là tập nghiệm của phương trình $x+5y=0$.

LG e

$4x + 0y = -2$

Phương pháp giải:

1) Tìm nghiệm tổng quát của phương trình:

+) Nếu $a \ne 0$ thì tìm $x$ theo $y$. Khi đó công thức nghiệm là:

$\left\{ \matrix{ x = \dfrac{c - by}{a} \hfill \cr y \in \mathbb{R} \hfill \cr} \right.$

+) Nếu $b \ne 0$ thì tìm $y$ theo $x$. Khi đó công thức nghiệm là:

$\left\{ \matrix{ y = \dfrac{c - ax}{b} \hfill \cr x \in \mathbb{R} \hfill \cr} \right.$

2) Cách vẽ đường thẳng có phuương trình: $ax+by=c$.

+) Nếu $a \ne 0,\ b \ne 0$ thì vẽ đường thẳng $y=\dfrac{-a}{b}x+\dfrac{c}{b}$

+) Nếu $a \ne 0,\ b=0$ thì vẽ đường thẳng $x=\dfrac{c}{a}$ song song hoặc trùng với trục tung.

+) Nếu $a =0,\ b \ne 0$ thì vẽ đường thẳng $y=\dfrac{c}{a}$ song song hoặc trùng với trục hoành.

Lời giải chi tiết:

Ta có phương trình $4x + 0y = -2 \Leftrightarrow 4x=-2 \Leftrightarrow x=\dfrac{-1}{2}$. Nghiệm tổng quát của phương trình là:

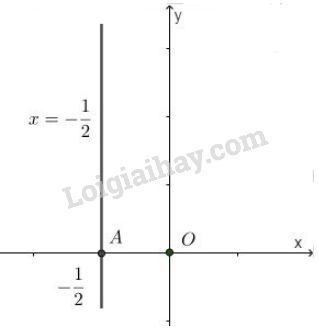
$\left\{\begin{matrix} x = -\dfrac{1}{2} & & \\ y \in R & & \end{matrix}\right.$

Tập nghiệm là đường thẳng $x = -\dfrac{1}{2}$ đi qua $A {\left(-\dfrac{1}{2}; 0 \right)}$ và song song với trục tung.

LG f

$0x + 2y = 5$

Phương pháp giải:

1) Tìm nghiệm tổng quát của phương trình:

+) Nếu $a \ne 0$ thì tìm $x$ theo $y$. Khi đó công thức nghiệm là:

$\left\{ \matrix{ x = \dfrac{c - by}{a} \hfill \cr y \in \mathbb{R} \hfill \cr} \right.$

+) Nếu $b \ne 0$ thì tìm $y$ theo $x$. Khi đó công thức nghiệm là:

$\left\{ \matrix{ y = \dfrac{c - ax}{b} \hfill \cr x \in \mathbb{R} \hfill \cr} \right.$

2) Cách vẽ đường thẳng có phuương trình: $ax+by=c$.

+) Nếu $a \ne 0,\ b \ne 0$ thì vẽ đường thẳng $y=\dfrac{-a}{b}x+\dfrac{c}{b}$

+) Nếu $a \ne 0,\ b=0$ thì vẽ đường thẳng $x=\dfrac{c}{a}$ song song hoặc trùng với trục tung.

+) Nếu $a =0,\ b \ne 0$ thì vẽ đường thẳng $y=\dfrac{c}{a}$ song song hoặc trùng với trục hoành.

Lời giải chi tiết:

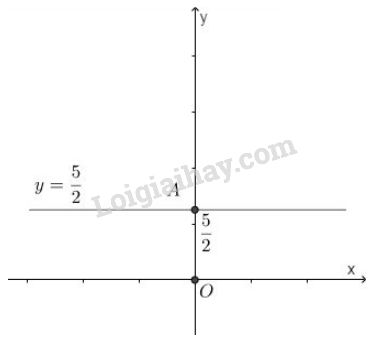
$0x + 2y = 5 \Leftrightarrow 2y=5 \Leftrightarrow y=\dfrac{5}{2}.$ Nghiệm tổng quát của phương trình là:

$\left\{\begin{matrix} x \in R & & \\ y = \dfrac{5}{2} & & \end{matrix}\right.$

Tập nghiệm là đường thẳng $y = \dfrac{5}{2}$ đi qua $A {\left( 0;\dfrac{5}{2} \right)}$ và song song với trục hoành.