Bài 1 trang 99 SGK Toán 9 tập 1
Cho hình chữ nhật ABCD có AB=12cm, BC=5cm. Chứng minh rằng bốn điểm A, B, C, D thuộc cùng một đường tròn...
Đề bài
Cho hình chữ nhật \(ABCD\) có \(AB=12cm,\ BC=5cm\). Chứng minh rằng bốn điểm \(A,\ B,\ C,\ D\) thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.
Phương pháp giải - Xem chi tiết
+) Để chứng minh nhiều điểm cùng nằm trên một đường tròn, ta chứng minh các điểm này cùng cách đều một điểm.
+) Sử dụng tính chất của hình chữ nhật: \(ABCD\) là hình chữ nhật, hai đường chéo cắt nhau tại \(O\) thì ta có \(OA=OB=OC=OD=\dfrac{AC}{2}=\dfrac{BD}{2}\).
+) Định lí Pytago: \(\Delta{ABC}\) vuông tại \(C\) thì \(BC^2=AB^2+AC^2.\)
Lời giải chi tiết
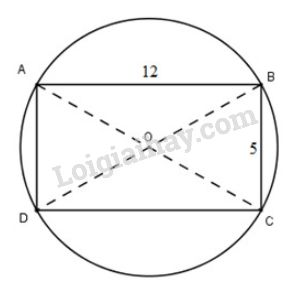
Gọi \(O\) là giao điểm hai đường chéo của hình chữ nhật, ta có \(OA = OB = OC = OD \) (tính chất) nên bốn điểm này cùng thuộc đường tròn tâm \(O\), bán kính \(R=OA\).
Xét tam giác \(ABC\) vuông tại \(B\), áp dụng định lí Pytago, ta có:
\(AC^{2}=AB^{2}+BC^{2}=12^{2}+5^{2}=169\)
\(\Rightarrow AC=\sqrt{169}=13\,cm\)
\(\Rightarrow R=OA=\dfrac{13}{2}=6,5\,cm\)
Vậy bán kính của đường tròn là: \(R=6,5\,cm.\)