Bài 1 trang 134 SGK Toán 9 tập 2 — Không quảng cáo

Đề bài

Chu vi hình chữ nhật $ABCD$ là $20cm$. Hãy tìm giá trị nhỏ nhất của độ dài đường chéo $AC$.

Lời giải chi tiết

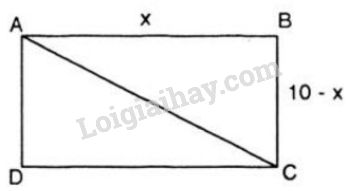
Gọi $x$ ($cm$) là độ dài cạnh $AB$

Vì  nửa chu vi hình chữ nhật đã cho là: $20:2=10 \, cm$ nên $AB+BC=10cm$ suy ra  $BC=10 – x \, (cm).$

Áp dụng định lí Py-ta-go trong tam giác vuông $ABC$, ta có:

$\eqalign{ & A{C^2} = A{B^2} + B{C^2} \cr & = {x^2} + {\left( {10 - x} \right)^2} \cr & = 2\left( {{x^2} - 10{\rm{x}} + 50} \right) \cr & = 2\left[ {{{\left( {x - 5} \right)}^2} + 25} \right] \cr}$

Vì $(x-5)^2 \geq 0, \forall x \in \mathbb{R}$

$\Rightarrow A{C^2} = 2{\left( {x - 5} \right)^2} + 50 \ge 50, \forall x \in \mathbb{R}$

Dấu "=" xảy ra khi : $x – 5 = 0 ⇔ x = 5$

Vậy giá trị nhỏ nhất của đường chéo AC là $\sqrt{50} = 5\sqrt2$ ($cm$)