Bài 2 trang 77 SGK Toán 11 tập 1 - Cánh Diều
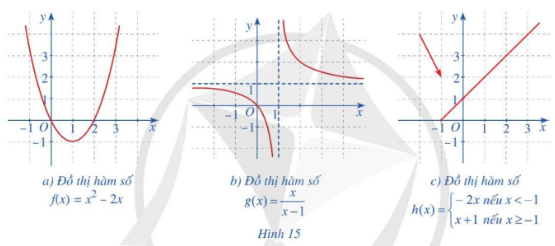
Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.
Đề bài
Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.
Phương pháp giải - Xem chi tiết
- Các hàm đa thức liên tục trên \(\mathbb{R}\)
- Các hàm phân thức hữu tỉ liên tục trên từng khoảng xác định của chúng
- Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Lời giải chi tiết
+) Hình 15a: Hàm số \(f\left( x \right) = {x^2}\;-2x\) có tập xác định \(D = \mathbb{R}.\)
Hàm số liên tục trên \(\mathbb{R}.\)
+) Hình 15b: Hàm số \(g\left( x \right) = \frac{x}{{x - 1}}\) có tập xác định \(D = \mathbb{R}\backslash \left\{ 1 \right\}.\)
Vậy hàm số liên tục trên các khoảng \(\left( {-\infty ;1} \right)\)và \(\left( {1; + \infty } \right).\)
+) Hình 15c:
Với \(x\; \in \;\left( {-\infty ;-1} \right)\) có \(f\left( x \right) = -2x\) liên tục với mọi \(x\; \in \;\left( {-\infty ;-1} \right)\)
Với \(x\; \in \;\left( {-1; + \infty } \right)\) có \(f\left( x \right) = x + 1\) liên tục với mọi \(x\; \in \;\left( {-1; + \infty } \right)\)
Tại x = – 1 có
\(\begin{array}{l}\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = \mathop {\lim }\limits_{x \to - 1} \left( {2x} \right) = 2.\left( { - 1} \right) = - 2\\f\left( { - 1} \right) = - 1 + 1 = 0\\ \Rightarrow \mathop {\lim }\limits_{x \to - 1} f\left( x \right) \ne f\left( { - 1} \right)\end{array}\)
Do đó hàm số không liên tục tại x = – 1.
Vậy hàm số liên tục trên các khoảng \(\left( {-\infty ;-1} \right)\)và \(\left( {-1; + \infty } \right).\)