Bài 3 trang 109 SGK Toán 11 tập 1 - Cánh Diều
Cho tứ diện ABCD. Lấy ({G_1},{G_2},{G_3})lần lượt là trọng tâm của các tam giác ABC, ACD, ADB.
Đề bài
Cho tứ diện ABCD . Lấy \({G_1},{G_2},{G_3}\)lần lượt là trọng tâm của các tam giác ABC, ACD, ADB.
a) Chứng minh rằng \(({G_1}{G_2}{G_3})//(BCD)\)
b) Xác định giao tuyến của mặt phẳng \(({G_1}{G_2}{G_3})\) với mặt phẳng \((ABD)\)
Phương pháp giải - Xem chi tiết
Nếu mặt phẳng (P) chứa hai đường thằng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q)
Lời giải chi tiết
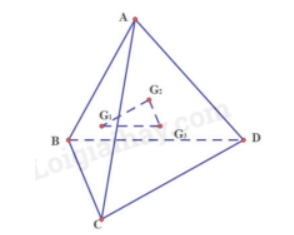
a) Gọi E, F, H là trung điểm của BC, CD, BD
Ta có:\({G_1}\) là trọng tâm tam giác ABC, suy ra\(\frac{{A{G_1}}}{{AE}} = \frac{2}{3}\)
\({G_3}\)là trọng tâm tam giác ABD, suy ra\(\frac{{A{G_3}}}{{AH}} = \frac{2}{3}\)
Suy ra tam giác AEH có\(\frac{{A{G_1}}}{{AE}} = \frac{{A{G_3}}}{{AH}}\) nên \({G_1}{G_3}//EH\)
Mà EH thuộc (BCD) nên \({G_1}{G_3}//(BCD)\)
Tương tự ta có:\({G_2}{G_3}//(BCD)\)
Do đó, \({G_1}{G_2}{G_3}//(BCD)\)
b)
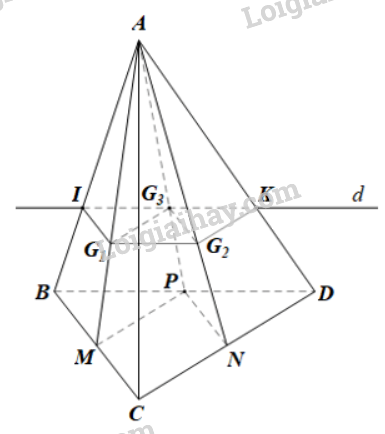
Ta có: B, D cùng thuộc hai mặt phẳng (ABD) và (BCD) nên \(\left( {ABD} \right) \cap \left( {BCD} \right) = BD\)
Giả sử \(\left( {ABD} \right) \cap \left( {{G_1}{G_2}{G_3}} \right) = d\)
Ta có:
\(\left\{ \begin{array}{l}\left( {{G_1}{G_2}{G_3}} \right)//(BCD)\\(ABD) \cap (BCD) = BD\\(ABD) \cap \left( {{G_1}{G_2}{G_3}} \right) = d\end{array} \right. \Rightarrow d//BD\)
Mà \({G_3} \in ({G_1}{G_2}{G_3})\) nên \({G_3}\) là giao điểm của \(({G_1}{G_2}{G_3})\) và (ABD)
Do đó giao tuyến d của hai mặt phẳng \(({G_1}{G_2}{G_3})\) và (ABD) đi qua \({G_3}\) và song song với BD, cắt AB, AD lần lượt tại I và K
Vậy \(({G_1}{G_2}{G_3}) \cap (ABD) = IK\)
Ta có: B, D cùng thuộc hai mặt phẳng (ABD) và (BCD) nên \(\left( {ABD} \right) \cap \left( {BCD} \right) = BD\)
Giả sử \(\left( {ABD} \right) \cap \left( {{G_1}{G_2}{G_3}} \right) = d\)
Ta có:
\(\left\{ \begin{array}{l}\left( {{G_1}{G_2}{G_3}} \right)//(BCD)\\(ABD) \cap (BCD) = BD\\(ABD) \cap \left( {{G_1}{G_2}{G_3}} \right) = d\end{array} \right. \Rightarrow d//BD\)
Mà \({G_3} \in ({G_1}{G_2}{G_3})\) nên \({G_3}\) là giao điểm của \(({G_1}{G_2}{G_3})\) và (ABD)
Do đó giao tuyến d của hai mặt phẳng \(({G_1}{G_2}{G_3})\) và (ABD) đi qua \({G_3}\) và song song với BD, cắt AB, AD lần lượt tại I và K
Vậy \(({G_1}{G_2}{G_3}) \cap (ABD) = IK\)