Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều — Không quảng cáo

Đề bài

Cho tứ diện ABCD . Gọi G là trọng tâm của tam giác ABD , điểm I nằm trên cạnh BC sao cho $BI = 2IC$. Chứng minh rằng IG song song với mặt phẳng (ACD).

Lời giải chi tiết

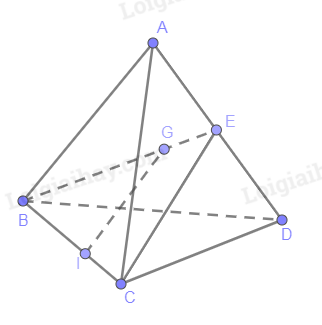
Tam giác BCE có E là trung điểm AD

Suy ra:$\frac{{BG}}{{BE}} = \frac{{BI}}{{BC}} = \frac{2}{3}$

Theo Ta lét, IG //CE

Mà CE thuộc (ACD)

Suy ra: IG // (ACD)