Bài 3 trang 94 SGK Toán 11 tập 2 - Cánh diều
Dốc là đoạn đường thẳng nối hai khu vực hay hai vùng có độ cao khác nhau. Độ dốc được xác định bằng góc giữa dốc và mặt phẳng nằm ngang
Đề bài
Dốc là đoạn đường thẳng nối hai khu vực hay hai vùng có độ cao khác nhau. Độ dốc được xác định bằng góc giữa dốc và mặt phẳng nằm ngang, ở đó độ dốc lớn nhất là 100%, tương ứng với góc \({90^ \circ }\) (độ dốc 10% tương ứng với góc \({9^ \circ }\)). Giả sử có hai điểm \(A,B\) nằm ở độ cao lần lượt là 200 m, 220 m so với mực nước biển và đoạn dốc \(AB\) dài 120 m. Độ dốc đó bằng bao nhiêu phần trăm (làm tròn kết quả đến hàng phần trăm?
Phương pháp giải - Xem chi tiết
‒ Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết
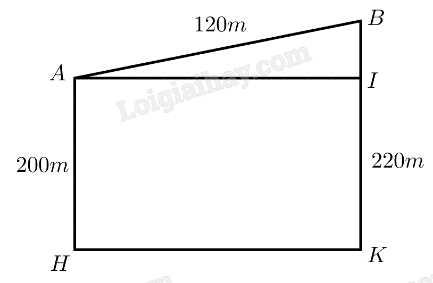
Mô hình hoá như hình vẽ, với \(AB\) là chiều dài con dốc, \(AH\) là độ cao của điểm \(A\) so với mặt nước biển, \(BK\) là độ cao của điểm \(B\) so với mặt nước biển, \(BI\) là chiều cao của con dốc, độ lớn của góc \(\widehat {BAI}\) chỉ độ dốc.
Ta có: \(AH = 200,BK = 220,AB = 120\).
\(AHKB\) là hình chữ nhật \( \Rightarrow IK = AH = 200 \Rightarrow BI = BK - IK = 220 - 200 = 20\)
Vì tam giác \(ABI\) vuông tại \(I\) nên ta có:
\(\sin \widehat {ABI} = \frac{{BI}}{{AB}} = \frac{{20}}{{120}} = \frac{1}{6} \Rightarrow \widehat {ABI} \approx 9,{59^ \circ }\) tương ứng với 10,66%
Vậy độ dốc của con dốc đó là 10,66%.