Bài 3 trang 99 SGK Toán 11 tập 1 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $O$ là giao điểm của $AC$ và $BD$; $M,N$ lần lượt là trung điểm của $SB,SD$; $P$ thuộc đoạn $SC$ và không là trung điểm của $SC$.

a) Tìm giao điểm $E$ của đường thẳng $SO$ và mặt phẳng $\left( {MNP} \right)$.

b) Tìm giao điểm $Q$ của đường thẳng $SA$ và mặt phẳng $\left( {MNP} \right)$.

c) Gọi $I,J,K$ lần lượt là giao điểm của $QM$ và $AB$, $QP$ và $AC$, $QN$ và $A{\rm{D}}$. Chứng minh $I,J,K$ thẳng hàng.

Lời giải chi tiết

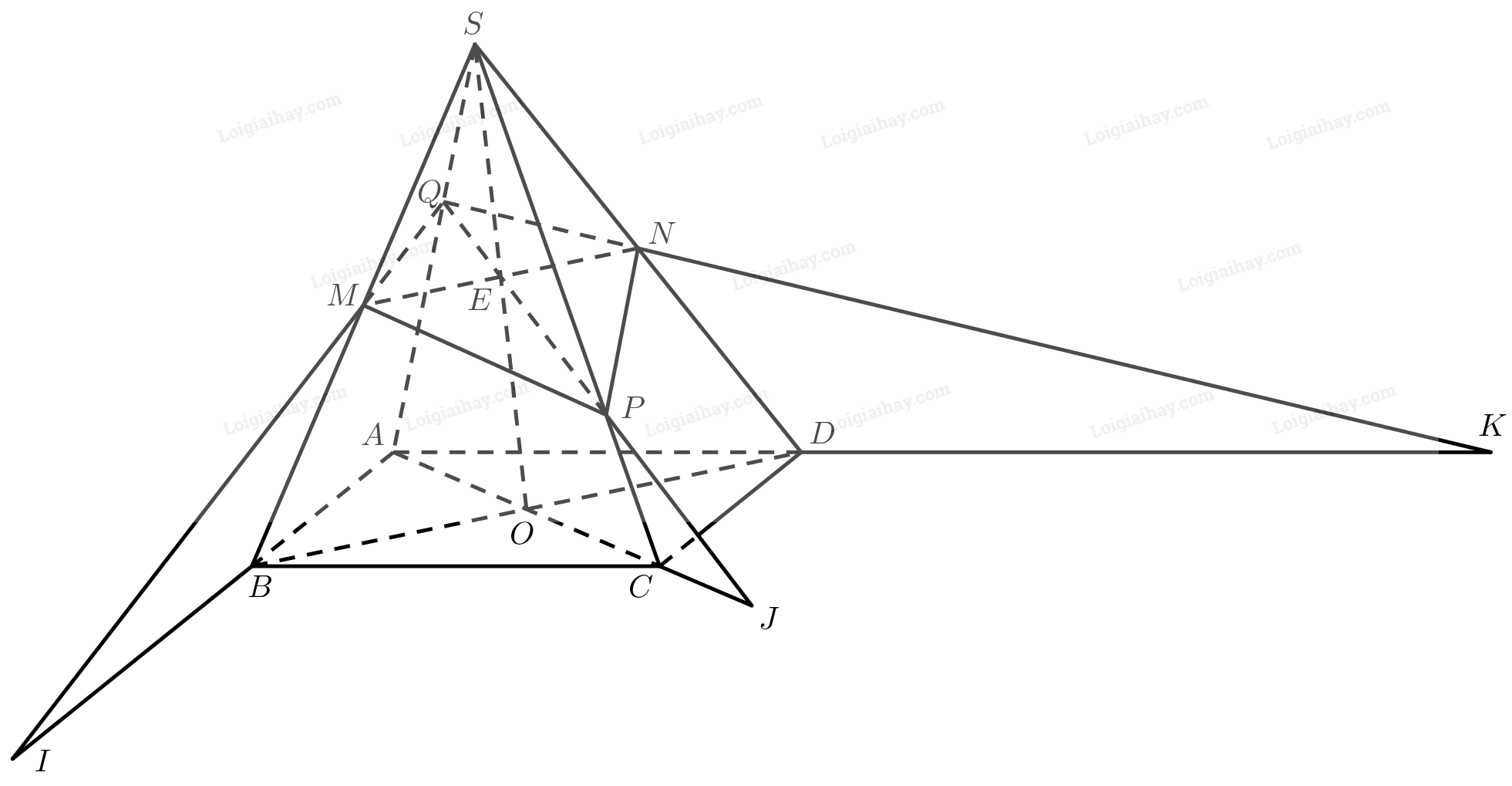
a) Gọi $E$ là giao điểm của $SO$ và $MN$. Ta có:

$\left. \begin{array}{l}E \in MN \subset \left( {MNP} \right)\\E \in S{\rm{O}}\end{array} \right\} \Rightarrow E = S{\rm{O}} \cap \left( {MNP} \right)$

b) Gọi $Q$ là giao điểm của $SA$ và $EP$. Ta có:

$\left. \begin{array}{l}Q \in EP \subset \left( {MNP} \right)\\Q \in S{\rm{A}}\end{array} \right\} \Rightarrow Q = S{\rm{A}} \cap \left( {MNP} \right)$

c) Ta có:

$\begin{array}{l}\left. \begin{array}{l}I \in QM \subset \left( {MNP} \right)\\I \in AB \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow I \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}J \in QP \subset \left( {MNP} \right)\\J \in AC \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow J \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}K \in QN \subset \left( {MNP} \right)\\K \in AD \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow K \in \left( {MNP} \right) \cap \left( {ABCD} \right)\end{array}$

Do đó, $I,J,K$ cùng nằm trên giao tuyến của hai mặt phẳng $\left( {MNP} \right)$ và $\left( {ABCD} \right)$.

Vậy $I,J,K$ thẳng hàng.