Bài 3 trang 85 SGK Toán 11 tập 2 – Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho hình chóp cụt lục giác đều \(ABCDEF.A'B'C'D'E'F'\) với \(O\) và \(O'\) là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là \(a\) và \(\frac{a}{2},OO' = a\)

a) Tìm góc giữa cạnh bên và mặt đáy.

b) Tìm góc phẳng nhị diện \(\left[ {O,AB,A'} \right];\left[ {O',A'B',A} \right]\).

Lời giải chi tiết

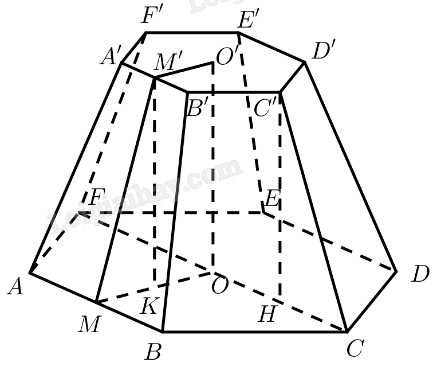
a) Kẻ \(C'H \bot OC\left( {H \in OC} \right)\)

là hình chữ nhật \( \Rightarrow OH = O'C' = a,OO'\parallel C'H\)

Mà \(OO' \bot \left( {ABCDEF} \right)\)

\(\begin{array}{l} \Rightarrow C'H \bot \left( {ABCDEF} \right)\\ \Rightarrow \left( {CC',\left( {ABCDEF} \right)} \right) = \left( {CC',CH} \right) = \widehat {C'CH}\end{array}\)

\(\begin{array}{l}HC = OC - O'C' = \frac{a}{2},C'H = OO' = a\\ \Rightarrow \tan \widehat {C'CH} = \frac{{C'H}}{{HC}} = 2 \Rightarrow \widehat {C'CH} \approx 63,{4^ \circ }\end{array}\)

Vậy \(\left( {CC',\left( {ABCDEF} \right)} \right) \approx 63,{4^ \circ }\)

b) Gọi \(M,M'\) lần lượt là trung điểm của \(AB,A'B'\).

\( \Rightarrow OM \bot AB,O'M' \bot A'B'\)

\(ABB'A'\) là hình thang cân \( \Rightarrow MM' \bot AB,MM' \bot A'B'\)

\( \Rightarrow \left[ {O,AB,A'} \right] = \widehat {OMM'},\left[ {O',A'B',A} \right] = \widehat {O'M'M}\)

Kẻ \(M'K \bot OM\left( {K \in OM} \right)\)

\(OO'M'K\) là hình chữ nhật \( \Rightarrow OK = O'K' = \frac{{A'B'\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{4},OO' = M'K = a\)

\(\begin{array}{l}OM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2},MK = OM - OK = \frac{{a\sqrt 3 }}{4}\\ \Rightarrow \tan \widehat {OMM'} = \frac{{M'K}}{{MK}} = \frac{4}{{\sqrt 3 }} \Rightarrow \widehat {OMM'} \approx 66,{6^ \circ }\\ \Rightarrow \widehat {O'M'M} = {180^ \circ } - \widehat {OMM'} = 113,{4^ \circ }\end{array}\)