Bài 33 trang 109 SGK Toán 11 tập 2 - Kết nối tri thức — Không quảng cáo

Đề bài

Cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có $AB = a,AA' = a\sqrt 2$. Gọi M, N lần lượt là trung điểm của cạnh $BB'$ và $CC'$. Mặt phẳng $\left( {A'MN} \right)$ cắt đường thẳng AB, AC tương ứng tại $H$ và $K$.

a) Chứng minh rằng $MN//HK$.

b) Tính theo a thể tích khối chóp $A'$. AHK .

Lời giải chi tiết

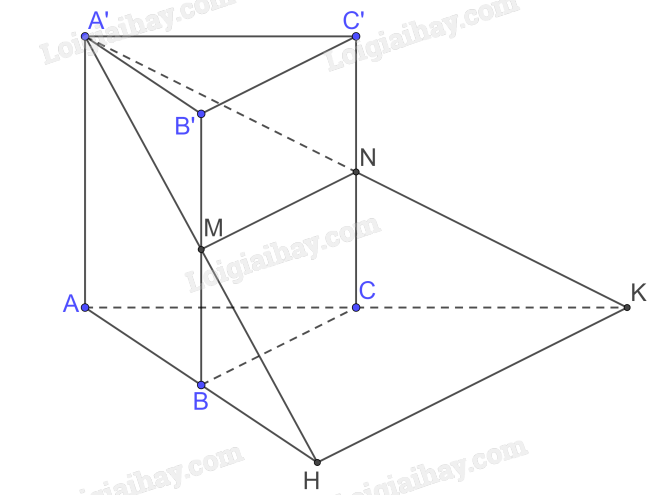
a) Dễ dàng chứng minh

$\Rightarrow BH = A'B',CK = A'C'$

Mà $AB = A'B',AC = A'C'$

Nên $AB = BH,AC = CK$

Do đó BC là đường trung bình tam giác AHK

$\Rightarrow BC//HK$

Ta có M, N lần lượt là trung điểm của cạnh $BB'$ và $CC'$ nên MN là đường trung bình của hình BB’C’C do đó MN // BC

Vậy MN // HK

b) Ta có AK = 2AC, AH = 2AB, HK = 2BC mà AB = AC = BC nên AK = AH = KH

Do đó tam giác AHK là tam giác đều cạnh 2a

$\Rightarrow {S_{AHK}} = {a^2}\sqrt 3$

Thể tích khối chóp $A'$. AHK là $V = \frac{1}{3}.AA'.{S_{AHK}} = \frac{1}{3}.a\sqrt 2 .{a^2}\sqrt 3  = \frac{{{a^3}\sqrt 6 }}{3}$