Bài 31 trang 109 SGK Toán 11 tập 2 - Kết nối tri thức — Không quảng cáo

Đề bài

Cho tứ diện OABC có $OA = OB = OC = a,\widehat {AOB} = \widehat {AOC} = {60^0}$ và $\widehat {BOC} = {90^0}$.

a) Chứng minh rằng $(OBC) \bot (ABC)$.

b) Tính theo a khoảng cách từ $O$ đến mặt phẳng $(ABC)$ và thể tích khối tứ diện OABC.

Lời giải chi tiết

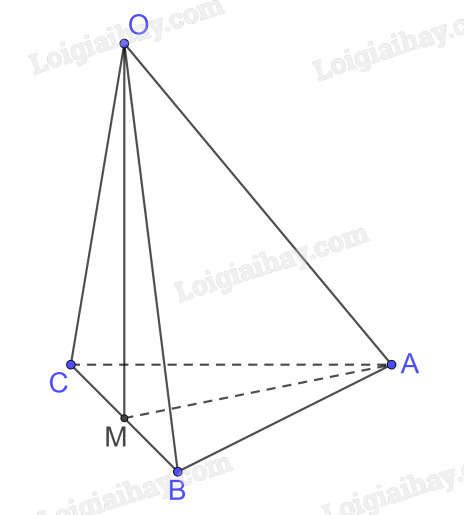
a) Gọi M là trung điểm của BC

Mà tam giác OCB cân tại O (do OB = OC)

Do đó $OM \bot BC$

Ta có tam giác OAC đều, tam giác OAB đều (do $OA = OB = OC = a,\widehat {AOB} = \widehat {AOC} = {60^0}$)

Do đó AC = AB = a.

Xét tam giác BOC vuông tại O ($\widehat {BOC} = {90^0}$) có

$\begin{array}{l}BC = \sqrt {O{B^2} + O{C^2}}  = a\sqrt 2 \\OM = \frac{1}{2}BC = \frac{{a\sqrt 2 }}{2}\end{array}$

Xét tam giác ABC có

$\begin{array}{l}A{C^2} + A{B^2} = 2{a^2},B{C^2} = {\left( {a\sqrt 2 } \right)^2} = 2{a^2}\\ \Rightarrow A{C^2} + A{B^2} = B{C^2}\end{array}$

Do đó tam giác ABC vuông tại A $\Rightarrow AM = \frac{1}{2}BC = \frac{{a\sqrt 2 }}{2}$

Xét tam giác OMA có

$\begin{array}{l}O{M^2} + A{M^2} = 2.{\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} = {a^2},O{A^2} = {a^2}\\ \Rightarrow O{M^2} + A{M^2} = O{A^2}\end{array}$

Do đó tam giác OMA vuông tại M $\Rightarrow OM \bot AM$

Mà $OM \bot BC$

$\Rightarrow OM \bot \left( {ABC} \right);OM \subset \left( {OBC} \right) \Rightarrow \left( {OBC} \right) \bot \left( {ABC} \right)$

b) Vì $OM \bot \left( {ABC} \right)$ nên $d\left( {O,\left( {ABC} \right)} \right) = OM = \frac{{a\sqrt 2 }}{2}$

${S_{\Delta ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}a.a = \frac{{{a^2}}}{2}$

Suy ra ${V_{O.ABC}} = \frac{1}{3}.OM.{S_{\Delta ABC}} = \frac{1}{3}.\frac{{a\sqrt 2 }}{2}.\frac{{{a^2}}}{2} = \frac{{{a^3}\sqrt 2 }}{{12}}$

Vậy $d\left( {O,\left( {ABC} \right)} \right) = \frac{{a\sqrt 2 }}{2}$; ${V_{O.ABC}} = \frac{{{a^3}\sqrt 2 }}{{12}}$