Bài 38 trang 129 SGK Toán 9 tập 2
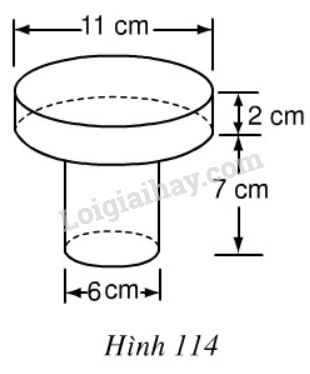
Hãy tính thể tích , diện tích bề mặt một chi tiết máy theo kích thước đã cho trên hình 114.
Đề bài
Hãy tính thể tích , diện tích bề mặt một chi tiết máy theo kích thước đã cho trên hình 114.
Phương pháp giải - Xem chi tiết
+) Diện tích xung quanh của hình trụ: \(S_{xq}=2\pi rh.\)
+) Diện tích toàn phần của hình trụ: \(S_{tp}=2 \pi rh +2 \pi r^2.\)
+) Thể tích hình trụ là: \(V=\pi r^2h.\)
Lời giải chi tiết
* Ta có: Thể tích phần cần tính là tổng thể tích của hai hình trụ có đường kính là \(11cm\), chiều cao là \(2cm\) và hình trụ có đường kính đáy là \(6cm\), chiều cao là \(7cm\):
\(\displaystyle {V_1} = \pi {R^2}{h_1} = \pi {\left( {{{11} \over 2}} \right)^2}.2 = 60,5\pi \left( {c{m^3}} \right)\)
\(\displaystyle {V_2} = \pi {R^2}{h_2} = \pi {\left( {{6 \over 2}} \right)^2}.7 = 63\pi \left( {c{m^3}} \right)\)
Vậy thể tích của chi tiết máy cần tính là:
\(V = {V_1} + {V_2} = 60,5\pi + 63\pi = 123,5\pi (c{m^3}) \approx 387,79 cm^3\)
* Tương tự, theo đề bài diện tích bề mặt của chi tiết máy bằng tổng diện tích xung quanh của hai hình trụ và diện tích 2 hình tròn đáy của hình trụ nằm trên = diện tích toàn phần của hình trụ trên + diện tích xung quanh của hình trụ dưới
Diện tích toàn phần của hình trụ có đường kính đáy \(11 cm\), chiều cao là \(2cm\) và là:
\({S_{tp(1)}} = 2\pi R_1{h_1} + 2\pi {R_1}^2 \)
\(\displaystyle = 2\pi {{11} \over 2}.2 + 2\pi .5,5^2 = 82,5 \pi \left( {c{m^2}} \right)\)
Diện tích xung quanh của hình trụ có đường kính đáy là \(6cm\) và chiều cao là \(7cm\) là:
\(\displaystyle {S_{xq(2)}} = 2\pi R_2 {h_2} = 2\pi {6 \over 2}.7 = 42\pi \left( {c{m^2}} \right)\)
Vậy diện tích bề mặt của chi tiết máy là:
\(S = {S_{tp(1)}} + {\rm{ }}{S_{xq(2)}} = 82,5\pi + 42\pi = 124,5\pi (c{m^2}) \approx 390,93 cm^2\)