Bài 42 trang 130 SGK Toán 9 tập 2
Hãy tính thể tích các hình dưới đây theo kích thước đã cho (h.117).
Đề bài
Hãy tính thể tích các hình dưới đây theo kích thước đã cho (h.117).
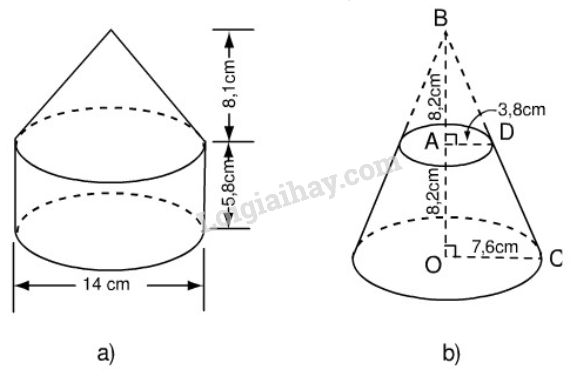
Phương pháp giải - Xem chi tiết
+) Thể tích hình trụ: \(V=\pi r^2 h.\)
+) Thể tích hình nón: \(V = \dfrac{1}{3}\pi {r^2}h.\)
+) Thể tích hình nón cụt: \( V_{hình \, \, nón \, \, cụt}=V_{hình \, \, nón \, \, lớn}- V_{hình \, \, nón \, \, nhỏ}. \)
Lời giải chi tiết
- Hình a:
Thể tích hình trụ có đường kính đáy \(14cm\), đường cao \(5,8cm\)
\({V_1} = {\rm{ }}\pi {\rm{ }}.{\rm{ }}{r^2}h{\rm{ }} = {\rm{ }}\pi .{\rm{ }}{7^2}.{\rm{ }}5,8{\rm{ }} = {\rm{ }}284,2{\rm{ }}\pi {\rm{ }}(c{m^3})\)
Thể tích hình nón có đường kính đáy \(14cm\) và đường cao \(8,1 cm\).
\(\displaystyle {V_2} = {1 \over 3}\pi {r^2}h = {1 \over 3}\pi {.7^2}.8,1 = 132,3\pi \left( {c{m^3}} \right)\)
Vậy thể tích hình cần tính là:
\(V{\rm{ }} = {\rm{ }}{V_1} + {\rm{ }}{V_2} = {\rm{ }}284,2\pi {\rm{ }} + {\rm{ }}132,3\pi {\rm{ }} = {\rm{ }}416,5\pi {\rm{ }}(c{m^3})\)
- Hình b:
Thể tích hình nón lớn có bán kính đáy là \(7,6 cm\), đường cao \(8,2+8,2=16,4 cm\) là: \(\displaystyle {V_1} = {1 \over 3}\pi {r^2}{h_1} = {1 \over 3}\pi {\left( {7,6} \right)^2}.16,4 = 991,47(c{m^3})\)
Thể tích hình nón nhỏ có bán kính đáy là \(3,8 cm\), đường cao \(8,2 cm\) là: \(\displaystyle {V_2} = {1 \over 3}\pi {r^2}{h_2} = {1 \over 3}\pi {\left( {3,8} \right)^2}.8,2 = 123,93(c{m^3})\)
Thể tích hình nón cụt cần tính là: \(\displaystyle V{\rm{ }} = {\rm{ }}{V_1}-{\rm{ }}{V_2} = {\rm{ }}991,47{\rm{ }}-{\rm{ }}123,93{\rm{ }} = {\rm{ }}867,54{\rm{ }}c{m^3}\)