Bài 5 trang 94 SGK Toán 11 tập 1 - Cánh diều
Cho hình chóp S.ABC. Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho \(MA = 2MS,NS = 2NC\) a) Xác định giao điểm của MN với mặt phẳng (ABC) b) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABC)
Đề bài
Cho hình chóp S.ABC . Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho \(MA = 2MS,NS = 2NC\)
a) Xác định giao điểm của MN với mặt phẳng (ABC)
b) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABC)
Phương pháp giải - Xem chi tiết
a) Muốn tìm giao điểm của một đường thẳng a và mặt phẳng (P) , ta tìm giao điểm của a và một đường thẳng b nằm trong (P) :
\(\left\{ \begin{array}{l}a \cap b = M\\b \subset (P)\end{array} \right. \Rightarrow M = a \cap (P)\)
Bước 1: Xác định mp (Q) chứa a
Bước 2: Tìm giao tuyến \(b = (P) \cap (Q)\)
Bước 3: Trong \((Q):a \cap b = M\) mà \(b \subset (P)\)suy ra \(M = a \cap (P)\)
b) Để xác định giao tuyến của hai mặt phẳng, ta tìm điểm chung của chúng.
b, Đường thẳng đi qua hai điểm chung là giao tuyến
Lời giải chi tiết
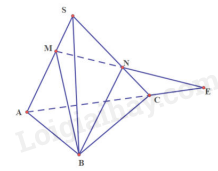
a) Tam giác SAC có: MN cắt AC tại E mà AC thuộc mp (ABC)
Do đó: E là giao điểm của MN và (ABC)
b) Ta có: B thuộc hai mặt phẳng (BMN) và (ABC)
E thuộc hai mặt phẳng (BMN) và (ABC)
Suy ra: BE là giao tuyến của hai mặt phẳng (BMN) và (ABC)