Bài 5 trang 99 SGK Toán 11 tập 2 - Cánh Diều
Cho hình chóp (S.ABCD) có đáy (ABCD) là hình chữ nhật, mặt phẳng (left( {SAB} right)) vuông góc với mặt đáy
Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, mặt phẳng \(\left( {SAB} \right)\) vuông góc với mặt đáy, tam giác \(SAB\) vuông cân tại \(S\). Gọi \(M\) là trung điểm của \(AB\). Chứng minh rằng:
a) \(SM \bot \left( {ABCD} \right)\);
b) \(AD \bot \left( {SAB} \right)\);
c) \(\left( {SAD} \right) \bot \left( {SBC} \right)\).
Phương pháp giải - Xem chi tiết
‒ Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
‒ Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Lời giải chi tiết
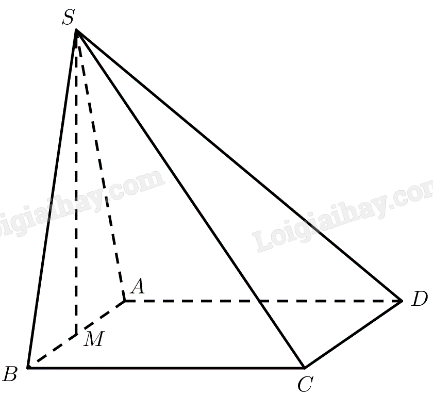
a, Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)
\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot AD\) (1)
Lại có \(SM \bot (ABCD) \Rightarrow SM \bot AD\) (2)
Mà \(SM,AB \subset (SAB)\) (3)
Từ (1), (2), (3) suy ra \(AD \bot (SAB)\).
c) \(AD \bot (SAB) \Rightarrow AD \bot SB\) (1)
Tam giác \(SAB\) vuông cân tại \(S\) nên \(SA \bot SB\) (2)
Mà \(SA,AD \subset (SAD)\) (3)
Từ (1), (2), (3) suy ra \(SB \bot (SAD)\).
Có \(\left\{ {\begin{array}{*{20}{c}}{SB \bot (SAD)}\\{SB \subset (SBC)}\end{array}} \right.\) suy ra \((SBC) \bot (SAD)\).