Bài 6.11 trang 19 SGK Toán 11 tập 2 - Cùng khám phá
Cho đồ thị của hai hàm số \(y = {\log _a}x\); \(y = {\log _b}x\) lần lượt là (C1) và (C2) (Hình 6.16).
Đề bài
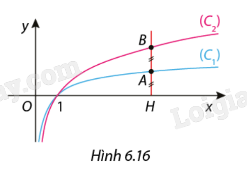
Cho đồ thị của hai hàm số \(y = {\log _a}x\); \(y = {\log _b}x\) lần lượt là (C 1 ) và (C 2 ) (Hình 6.16). Tìm hệ thức liên hệ giữa a và b, biết mọi đường thẳng song song với trục tung, cắt trục hoành, (C 1 ), (C 2 ) lần lượt tại H, A, B thì A là trung điểm của BH.
Phương pháp giải - Xem chi tiết
A là trung điểm của BH nên \({y_B} = 2{y_A}\)
Theo đồ thị trên hình vẽ thì \({x_A} = {x_B} = {x_H}\)
Áp dụng: \({\log _a}b = c \Leftrightarrow {a^c} = b\).
Lời giải chi tiết
Gọi điểm \(H\left( {{x_H};0} \right)\), \(A\left( {{x_A};{y_A}} \right)\), \(B\left( {{x_B};{y_B}} \right)\)
A là trung điểm của BH nên \({y_B} = 2{y_A}\)
Theo đồ thị trên hình vẽ thì \({x_A} = {x_B} = {x_H}\)
Ta có điểm A thuộc (C 1 ) nên \({y_A} = {\log _a}{x_A} \Leftrightarrow {a^{{y_A}}} = {x_A}\)
Điểm B thuộc (C 2 ) nên \({y_B} = {\log _b}{x_B} \Leftrightarrow {b^{{y_B}}} = {x_B} \Leftrightarrow {b^{2{y_A}}} = {x_A}\)
\( \Rightarrow {\left( {{b^2}} \right)^{{y_A}}} = {a^{{y_A}}} \Leftrightarrow {b^2} = a\)