Bài 6.10 trang 19 SGK Toán 11 tập 2 - Cùng khám phá
Tìm hàm số \(y = C.{a^x}\) mà đồ thị của nó được biểu diễn dưới đây:
Đề bài
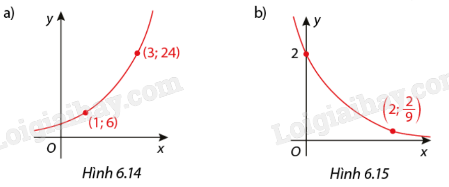
Tìm hàm số \(y = C.{a^x}\) mà đồ thị của nó được biểu diễn dưới đây:
Phương pháp giải - Xem chi tiết
Đồ thị đi qua 2 điểm A(a; b), B (c; d). Thay tọa độ các điểm vào hàm số để tìm C, a.
Lời giải chi tiết
a) Đồ thị hàm số với a >1, đi qua 2 điểm (1; 6) và (3; 24). Ta có:
\(\left\{ \begin{array}{l}C.{a^1} = 6\\C.{a^3} = 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C.a = 6\\C.{a^3} = 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C.a = 6\\{a^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}a = 2\\a = - 2\,\left( {\rm{L}} \right)\end{array} \right.\\C.a = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\C = 3\end{array} \right.\)
Vậy hàm số cần tìm là \(y = {3.2^x}\).
b) Đồ thị hàm số với 0 < a < 1, đi qua 2 điểm \(\left( {2;\frac{2}{9}} \right)\) và \(\left( {0;2} \right)\). Ta có:
\(\left\{ \begin{array}{l}C.{a^2} = \frac{2}{9}\\C.{a^0} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C.{a^2} = \frac{2}{9}\\C = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} = \frac{1}{9}\\C = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}a = \frac{1}{3}\\a = - \frac{1}{3}\left( {\rm{L}} \right)\end{array} \right.\\C = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{3}\\C = 2\end{array} \right.\)
Vậy hàm số cần tìm là \(y = 2.{\left( {\frac{1}{3}} \right)^x}\)