Bài 6 trang 65 SGK Toán 11 tập 1 - Cánh Diều
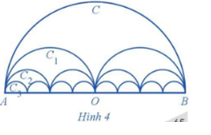
Gọi C là nửa đường tròn đường kính AB = 2R, C1 là đường gồm hai nửa đường tròn đường kính (frac{{AB}}{2},) C2 là đường gồm bốn nửa đường tròn đường kính (frac{{AB}}{4},...) Cn là đường gồm 2n nửa đường tròn đường kính (frac{{AB}}{{{2^n}}},...) (Hình 4). Gọi pn là độ dài của Cn, Sn là diện tích hình phẳng giới hạn bởi Cn và đoạn thẳng AB. a) Tính pn, Sn. b) Tìm giới hạn của các dãy số (pn) và (Sn).
Đề bài
Gọi C là nửa đường tròn đường kính AB = 2R, C 1 là đường gồm hai nửa đường tròn đường kính \(\frac{{AB}}{2},\), C 2 là đường gồm bốn nửa đường tròn đường kính \(\frac{{AB}}{4},...\)
Gọi p n là độ dài của C n , S n là diện tích hình phẳng giới hạn bởi C n và đoạn thẳng AB.
a) Tính p n , S n .
b) Tìm giới hạn của các dãy số (p n ) và (S n ).
Phương pháp giải - Xem chi tiết
Chu vi hình tròn \(C = \pi d\)
Diện tích hình tròn \(S = \pi {R^2}\)
Lời giải chi tiết
a) Vì C n là nửa đường tròn đường kính \(\frac{{AB}}{{{2^n}}}\) nên ta có \({p_n} = \frac{1}{2}{.2^n}.\frac{{AB}}{{{2^n}}}.\pi = {2^n}.\frac{R}{{{2^n}}}.\pi = \pi R\)
Đường kính \(\frac{{AB}}{{{2^n}}} = \frac{{2R}}{{{2^n}}}\) nên bánh kính \(\frac{R}{{{2^n}}}\)
\({S_n} = {2^n}.{\left( {\frac{R}{{{2^n}}}} \right)^2}.\frac{\pi }{2} = \frac{{\pi {R^2}}}{2}.\frac{1}{{{2^n}}} = \frac{{\pi {R^2}}}{{{2^{n + 1}}}}\)
b) \(\begin{array}{l}\lim {p_n} = \lim \left( {\pi R} \right) = \pi R\\\lim {S_n} = \lim \frac{{\pi {R^2}}}{{{2^{n + 1}}}} = \lim \left[ {\frac{{\pi {R^2}}}{2}.{{\left( {\frac{1}{2}} \right)}^n}} \right] = \lim \frac{{\pi {R^2}}}{2}.\lim {\left( {\frac{1}{2}} \right)^n} = 0\end{array}\)