Bài 6 trang 94 SGK Toán 11 tập 2 - Cánh diều — Không quảng cáo

Đề bài

Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$. Gọi $\alpha$ là số đo của góc nhị diện $\left[ {A,BC,S} \right]$. Chứng minh rằng tỉ số diện tích của hai tam giác $ABC$ và $SBC$ bằng $\cos \alpha$.

Lời giải chi tiết

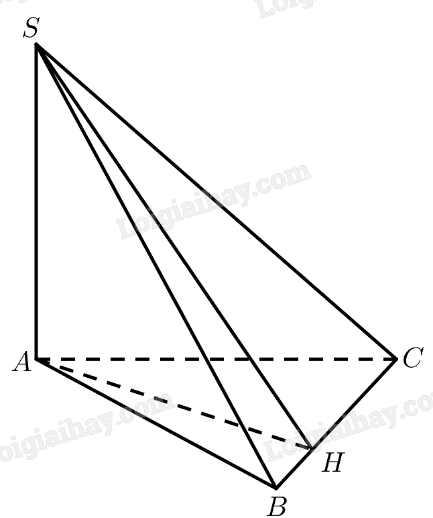
Kẻ $AH \bot BC\left( {H \in BC} \right)$

$SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC$

$\Rightarrow BC \bot \left( {SAH} \right) \Rightarrow BC \bot SH$

Vậy $\widehat {SHA}$ là góc phẳng nhị diện của góc nhị diện $\left[ {A,BC,S} \right]$

$\Rightarrow \widehat {SHA} = \alpha$

$\begin{array}{l}{S_{\Delta ABC}} = \frac{1}{2}BC.AH,{S_{\Delta SBC}} = \frac{1}{2}BC.SH\\ \Rightarrow \frac{{{S_{\Delta ABC}}}}{{{S_{\Delta SBC}}}} = \frac{{\frac{1}{2}BC.AH}}{{\frac{1}{2}BC.SH}} = \frac{{AH}}{{SH}} = \cos \widehat {SHA} = \cos \alpha \end{array}$