Bài 7 trang 69 SGK Toán 9 tập 2 — Không quảng cáo

Đề bài

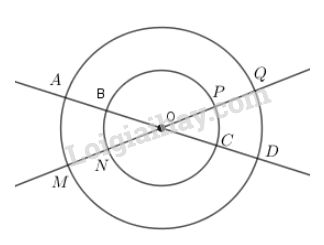
Cho hai đường tròn cùng tâm \(O\) với bán kính khác nhau. Hai đường thẳng đi qua \(O\) cắt hai đường tròn đó tại các điểm \(A, B, C, D, M, N, P, Q\) (h.8)

a)Em có nhận xét gì về số đo của các cung \(AM, CP, BN, DQ\).

b) Hãy nêu tên các cung nhỏ bằng nhau.

c) Hãy nêu tên hai cung lớn bằng nhau.

Lời giải chi tiết

a) Các cung nhỏ \(\overparen{AM}, \overparen{CP}, \overparen{BN}, \overparen{DQ}\) có cùng số đo (cùng bằng góc BON)

b) \(\overparen{AM}\) = \(\overparen{DQ}\); \(\overparen{BN}\) = \(\overparen{PC}\); \(\overparen{AQ}\) =\(\overparen{ MD}\); \(\overparen{BP}\) =\(\overparen{NC}\).

c) Các cung lớn bằng nhau:

\(\overparen{AMDQ} = \overparen{MAQD}\); \(\overparen{BNCP} = \overparen{NBPC}\)

Chú ý:

+ Phân biệt "so sánh hai cung" và "so sánh số đo hai cung":

Ta chỉ so sánh được hai cung trong cùng một đường tròn hoặc trong hai đường tròn bằng nhau.

So sánh số đo hai cung : luôn so sánh được

+ Ở câu c, ta có thể chọn 2 cung lớn bằng nhau khác, chẳng hạn: \(\overparen{AQDM} = \overparen{DMAQ}\); \(\overparen{BPCN} = \overparen{CNBP}\)