Bài 7 trang 69 SGK Toán 9 tập 1
Người ta đưa ra hai cách vẽ đoạn trung bình nhân x của hai đoạn thẳng a, b.
Đề bài
Người ta đưa ra hai cách vẽ đoạn trung bình nhân \(x\) của hai đoạn thẳng \(a,\ b\) (tức là \({x^2} = ab\) ) như trong hai hình sau:
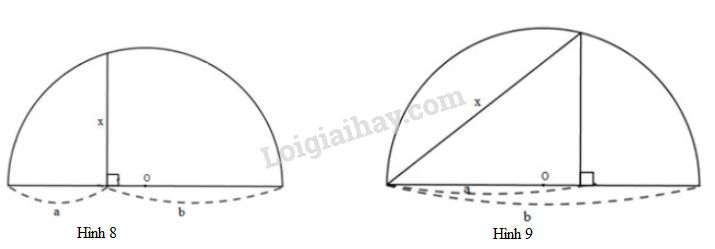
Dựa vào các hệ thức (1) và (2), hãy chứng minh các cách vẽ trên là đúng.
Gợi ý: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.
Phương pháp giải - Xem chi tiết
+) Đặt tên các điểm và nối các điểm lại để xuất hiện tam giác.
+) Dùng dấu hiệu: "tam giác có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh đó là tam giác vuông" để chứng minh tam giác vuông.
+ Dùng các hệ thức sau để chứng minh \(x\) là trung bình nhân của \(a,\ b\):
\(b^2=a.b',\ c^2=a.c'\) \((1)\)
\(h^2=b'.c'\) \((2)\)
+) Nêu các bước để vẽ được đoạn trung bình nhân.
Lời giải chi tiết
Cách 1: Đặt tên các đoạn thẳng như hình bên.
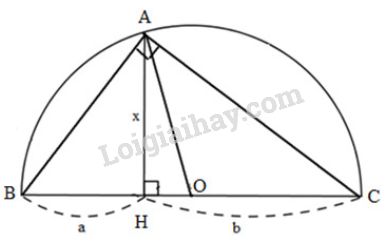
Xét \(\Delta{ABC}\) có:
\(OA = OB = OC = \dfrac{BC}{2}\) (cùng bằng bán kính đường tròn (O))
Mà \(AO\) là trung tuyến ứng với cạnh \(BC\) của \(\Delta{ABC}\).
Suy ra \(\Delta{ABC}\) vuông tại \(A\) ( tam giác có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền thì là tam giác vuông)
Xét \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\). Áp dụng hệ thức \(h^2=b'.c'\), ta được:
\(AH^2=BH.CH \Leftrightarrow x^2=a.b\)
\(\Leftrightarrow x=\sqrt {ab}\)
Vậy \(x\) là trung bình nhân của \(a\) và \(b\).
Cách vẽ : Bước \(1\): Đặt \(BH=a,\ CH=b\). Xác định trung điểm \(O\) của đoạn \(AB\).
Bước \(2\): Vẽ nửa đường tròn tâm \(O\) bán kính \(OB\).
Bước \(3\): Kẻ thẳng đi qua \(H\) và vuông góc với \(BC\). Đường thẳng này cắt nửa đường tròn tại \(A\).
Bước \(4\): Nối \(A\) và \(H\) ta được \(AH=x\) là đoạn trung bình nhân của hai đoạn thẳng \(a,\ b\).
Cách 2 : Vẽ và đặt tên như hình bên dưới
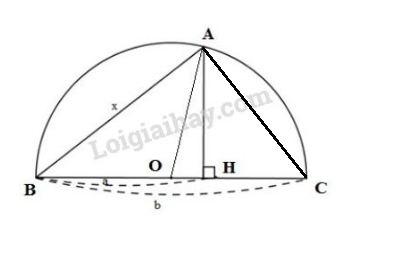
Xét \(\Delta{ABC}\) có:
\(OA = OB = OC = \dfrac{BC}{2} \) (cùng bằng bán kính đường tròn (O) )
Mà \(AO\) là trung tuyến ứng với cạnh \(BC\) của \(\Delta{ABC}\).
Suy ra \(\Delta{ABC}\) vuông tại \(A\) (tam giác có đường trung tuyến ứng với cạnh huyền bẳng nửa cạnh đó thì là tam giác vuông)
Xét \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\). Áp dụng hệ thức \(b^2=b'.a\), ta có:
\(AB^2 = BC.BH \Leftrightarrow x^2=a.b\)
\(\Leftrightarrow x=\sqrt{ab}\)
Vậy \(x\) là trung bình nhân của \(a\) và \(b\).
Cách vẽ: Bước \(1\): Đặt \(BH=a,\ CH=b\). Xác định trung điểm \(O\) của đoạn \(BC\).
Bước \(2\): Vẽ nửa đường tròn tâm \(O\) bán kính \(OB\).
Bước \(3\): Kẻ đường thẳng đi qua điểm \(H\) và vuông góc với \(BC\). Đường thẳng này cắt nửa đường tròn tại \(A\).
Bước \(4\): Nối \(B\) và \(A\) ta được \(AB=x\) là đoạn trung bình nhân của hai đoạn thẳng \(a,\ b\).