Bài 89 trang 104 SGK Toán 9 tập 2 — Không quảng cáo

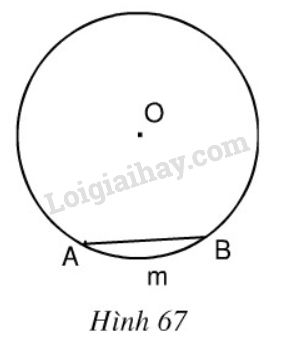
Trong hình 67, cung $AmB$ có số đo là $60^0$. Hãy:

a) b) c)

a) Vẽ góc ở tâm chắn cung $AmB$. Tính góc $AOB$.

b) Vẽ góc nội tiếp đỉnh $C$ chắn cung $AmB$. Tính góc $ACB$.

c) Vẽ góc tạo bởi tia tiếp tuyến $Bt$ và dây cung $BA$. Tính góc $ABt$.

Phương pháp giải:

- Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn. Số đo góc ở tâm bằng số đo cung bị chắn.

- Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn. Số đo góc nội tiếp bằng nửa số đo cung bị chắn

- Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh tại tiếp điểm, một cạnh là tia tiếp tuyến và cạnh kia chứa dây cung. Số đo góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo cung bị chắn.

Lời giải chi tiết:

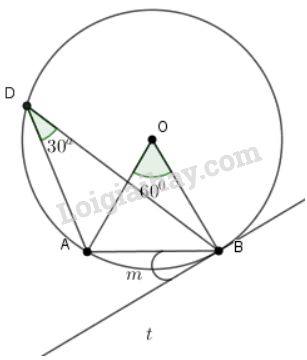
a) Từ $O$ nối với hai đầu mút của cung $AB$

Ta có $\widehat {AOB}$ là góc ở tâm chắn cung $AB$

Vì $\widehat {AOB}$ là góc ở tâm chắn cung $AB$ nên

$\widehat {AOB}$ =$sđ\overparen{AmB}=60^0$

b) Lấy một điểm $C$ bất kì trên $(O)$. Nối $C$ với hai đầu mút của cung $AmB$. Ta được góc nội tiếp $\widehat {ACB}$

Khi đó: $\displaystyle \widehat {ACB} = {1 \over 2}sđ\overparen{AmB}={1 \over 2}{60^0} = 30^0$

c) Vẽ bán kính $OB$. Qua $B$ vẽ $Bt\bot OB$. Ta được góc $ABt$ là góc tạo bởi tia tiếp tuyến $Bt$ với dây cung $BA$.

Ta có: $\displaystyle \widehat {ABt} = {1 \over 2}sđ\overparen{AmB} = {30^0}$

d) e)

d) Vẽ góc $ADB$ có đỉnh $D$ ở bên trong đường tròn. So sánh $\widehat {A{\rm{D}}B}$  với $\widehat {ACB}$ .

e) Vẽ góc $AEB$ có đỉnh $E$ ở bên ngoài đường tròn ($E$ và $C$ cùng phía đối với $AB$). So sánh $\widehat {A{\rm{E}}B}$ với $\widehat {ACB}$

Phương pháp giải:

- Góc có đỉnh bên trong và bên ngoài đường tròn (xem lại SGK toán 9 tập 2 trang 80). Số đo góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn, số đo góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

Lời giải chi tiết:

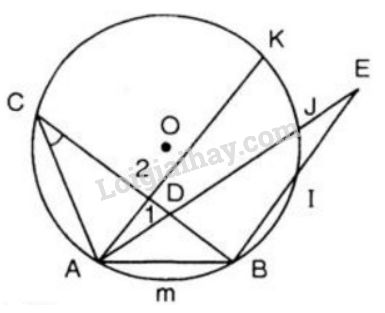
d) Lấy điểm $D$ bất kì ở bên trong đường tròn $(O)$. Nối $D$ với $A$ và $D$ với $B$, ta được góc $ADB$ là góc có đỉnh ở bên trong đường tròn $(O)$

Đường thẳng AD cắt đường tròn tại điểm thứ hai là K, DB cắt đường tròn tại điểm thứ hai là C.

Ta có:

$\eqalign{ & \widehat {ACB} = {1 \over 2}sđ\overparen{AmB}\cr & \widehat {A{\rm{D}}B} = {1 \over 2}\left( sđ\overparen{AmB}+ sđ\overparen{CK} \right) \cr}$

Mà $sđ\overparen{AmB}+sđ\overparen{CK}>sđ\overparen{AmB}$(do $sđ\overparen{CK}>0$) nên $\widehat {A{\rm{D}}B} > \widehat {ACB}$

e) Lấy điểm $E$ bất kì ở bên ngoài đường tròn, nối $E$ với $A$ và $E$ với $B$, chúng cắt đường tròn lần lượt tại $J$ và $I$.

Ta có

$\widehat {ACB} = {1 \over 2}sđ\overparen{AmB}$ (góc nội tiếp chắn cung AmB) $\widehat {A{\rm{E}}B} = {1 \over 2}\left( sđ\overparen{AmB} - sđ\overparen{IJ} \right)$ (góc có đỉnh nằm ngoài đường tròn)

Mà $sđ\overparen{AmB}$– $sđ \overparen{IJ}< sđ\overparen{AmB}$ (do $sđ\overparen{IJ}> 0$)

Nên $\widehat {A{\rm{E}}B} < \widehat {ACB}$.