Bài 9 trang 70 SGK Toán 9 tập 2
Trên đường tròn tâm O lấy ba điểm A, B, C
Đề bài
Trên đường tròn tâm \(O\) lấy ba điểm \(A, B, C\) sao cho \(\widehat{AOB} = 100^0\), sđ cung \(\overparen{AC} = 45^0\). Tính số đo của cung nhỏ \(\overparen{BC}\) và cung lớn \(\overparen{BC}\). (Xét cả hai trường hợp: điểm \(C\) nằm trên cung nhỏ \(\overparen{AB}\), điểm \(C\) nằm trên cung lớn \(\overparen{AB}\)).
Phương pháp giải - Xem chi tiết
Sử dụng:
+ Nếu \(C\) là một điểm nằm trên cung \(AB\) thì số đo cung \(AB = \)số đo cung \(AC + \) số đo cung \(BC\).
+ Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+ Số đo của cung lớn bằng hiệu giữa \({360^o}\) và số đo của cung nhỏ (có chung hai mút với cung lớn)
Lời giải chi tiết
TH1: Điểm \(C\) nằm trên cung nhỏ \(\overparen{AB}\)
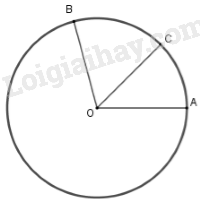
Số đo cung nhỏ BC là \(sđ \overparen{BC} = sđ \overparen{AB}-sđ \overparen{AC}= 100^0 – 45^0 = 55^0\)
Số đo cung lớn \(\overparen{BC} = 360^0 – 55^0 = 305^0\)
TH2: Điểm \(C\) nằm trên cung lớn \(\overparen{AB}\)
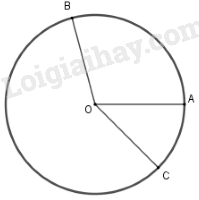
Số đo cung nh ỏ BC là \(sđ \overparen{BC} = sđ \overparen{AB}+sđ \overparen{AC}= 100^0 + 45^0= 145^0\)
Số đo cung lớn \(\overparen{BC} = 360^0 – 145^0 = 215^0\)