Câu 10 trang 13 SGK Hình học 11 Nâng cao
Cho hai điểm B,C cố định nằm trên đường tròn
Đề bài
Cho hai điểm B,C cố định nằm trên đường tròn và điểm A thay đổi trên đường tròn đó. Hãy dùng phép đối xứng trục để chứng minh rằng trực tâm H của tam giác ABC nằm trên một đường tròn cố định
Hướng dẫn : Khi BC không phải là đường kính, gọi H’ là giao điểm của đường thẳng AH với đường tròn (O; R). Chứng minh rằng H đối xứng với H’ qua đường thẳng BC.
Lời giải chi tiết
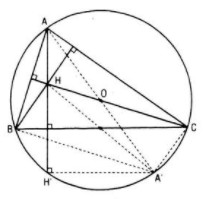
Trường hợp BC là đường kính thì tam giác ABC vuông tại A nên H trùng A
Do đó H nằm trên đường tròn cố định (O ; R)
Xét trường hợp BC không là đường kính.
Giả sử đường thẳng AH cắt đường tròn (O ; R) tại H’.
Gọi AA’ là đường kính của đường tròn (O ; R) thì:
A’B // CH (vì cùng vuông góc với AB)
A’C // BH (vì cùng vuông góc với AC)
Do đó A’BHC là hình bình hành.
Vậy BC đi qua trung điểm của HA’
Mặt khác BC // A’H’ (vì cùng vuông góc với AH) nên BC cũng đi qua trung điểm của HH’
(do BC đi qua trung điểm của HA' và song song A'H' nên đi qua trung điểm của HH')
Do đó H và H’ đối xứng với nhau qua BC.
Nếu gọi Đ là phép đối xứng có trục là đường thẳng BC thì Đ biến H’ thành H.
Nhưng H’ luôn luôn nằm trên (O ; R) nên H nằm trên đường tròn cố định là ảnh của đường tròn (O ; R) qua phép đối xứng trục Đ
Cách khác: Gọi H’ là điểm đối xứng của H qua BC. Chứng minh tứ giác ABH’C nội tiếp, từ đó suy ra H’ nằm trên (O ; R).