Câu 22 trang 30 SGK Đại số và Giải tích 11 Nâng cao — Không quảng cáo

Đề bài

Tính các góc của tam giác $ABC$, biết $AB = \sqrt 2  cm$, $AC =\sqrt 3  cm$ và đường cao $AH = 1cm$. (Gợi ý : Xét trường hợp $B, C$ nằm khác phía đối với $H$ và trường hợp $B, C$ nằm cùng phía đối với $H$).

Lời giải chi tiết

Ta xét hai trường hợp :

a/ $B$ và $C$ nằm khác phía đối với $H$

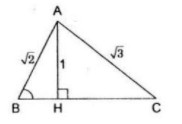
Trong tam giác vuông $ABH$ ta có :

$\sin B = {{AH} \over {AB}} = {1 \over {\sqrt 2 }}$

Suy ra $\widehat B = 45^\circ$ (chú ý rằng góc $B$ nhọn)

Trong tam giác $ACH$ ta có :

$\sin C = {{AH} \over {AC}} = {1 \over {\sqrt 3 }},$ suy ra $\widehat C \approx 35^\circ 15'52$

Từ đó  $\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right) \approx 99^\circ 44'8$

b/ $B$ và $C$ nằm cùng phía đối với $H$

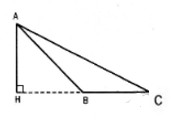
Tương tự như trên ta có:

$\sin \widehat {ABH} = \frac{{AH}}{{AB}} = \frac{1}{{\sqrt 2 }}$ $\Rightarrow \widehat {ABH} = {45^0}$

$\eqalign{ & \widehat {ABC} = 180^\circ - \widehat {ABH} \cr&= 180^\circ - 45^\circ = 135^\circ \cr }$

$\sin \widehat {ACH} = \frac{{AH}}{{AC}} = \frac{1}{{\sqrt 3 }}$ $\Rightarrow \widehat {ACH} = {35^0}15'52''$

Từ đó $\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right) \approx 9^\circ 44'8$