Câu 24 trang 111 SGK Hình học 11 Nâng cao
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và SA ⊥ (ABCD), SA = x. Xác định x để hai mặt phẳng (SBC) và (SDC) tạo với nhau góc 60˚.
Đề bài
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và SA ⊥ (ABCD), SA = x. Xác định x để hai mặt phẳng (SBC) và (SDC) tạo với nhau góc 60˚.
Lời giải chi tiết
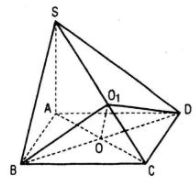
Gọi O là giao điểm của AC và BD. Trong mặt phẳng (SAC) kẻ OO 1 vuông góc với SC.
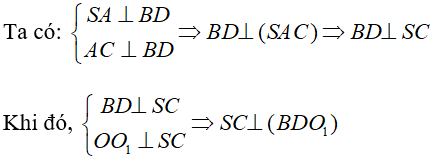
Vậy góc giữa hai mp(SBC) và (SDC) bằng góc giữa hai đường thẳng BO 1 và DO 1 .
Mặt khác OO 1 ⊥ BD, OO 1 < OC (vì OC là cạnh huyền của \(\Delta O{O_1}C\) vuông tại O1) mà OC = OB nên \(\widehat {B{O_1}O} > 45^\circ .\)
Tương tự \(\widehat {D{O_1}O} > 45^\circ \) tức \(\widehat {B{O_1}D} >90^\circ \)
Như vậy hai mặt phẳng (SBC) và (SDC) tạo với nhau góc \(60^\circ \) khi và chỉ khi:
\(\widehat {B{O_1}D} =120^\circ \) \( \Leftrightarrow\) \(\widehat {B{O_1}O} = 60^\circ \) (vì ΔBO 1 D cân tại O 1 )
\( \Leftrightarrow BO = O{O_1}\tan 60^\circ \) \(\Leftrightarrow BO = O{O_1}\sqrt 3 \)
Ta có \(O{O_1} \bot SC\) nên \(\widehat {O{O_1}C} = {90^0}\)
Xét tam giác \(CO{O_1}\) vuông tại \({O_1}\) có:
\(O{O_1} = OC\sin \widehat {OC{O_1}} = OC\sin \widehat {ACS}\) \( = OC.{{SA} \over {SC}}\)
Như vậy : \(BO = O{O_1}\sqrt 3 \Leftrightarrow BO = \sqrt 3 .OC.{{SA} \over {SC}} \) \(\Leftrightarrow SC = \sqrt 3 .SA\)
\( \Leftrightarrow \sqrt {{x^2} + 2{a^2}} = \sqrt 3 .x \Leftrightarrow x = a\)
Vậy khi x = a thì hai mặt phẳng (SBC) và (SDC) tạo với nhau góc 60˚