Câu 24 trang 227 SGK Đại số và Giải tích 11 Nâng cao
Cho hyperbol (H) xác định bởi phương trình
Cho hyperbol (H) xác định bởi phương trình \(y = {1 \over x}\)
LG a
Tìm phương trình tiếp tuyến (T) của (H) tại tiếp điểm A có hoành độ a (với a ≠ 0)
Lời giải chi tiết:
Với mọi x ≠ 0, ta có : \(f'\left( x \right) = - {1 \over {{x^2}}}\)
Phương trình tiếp tuyến (T) tại điểm \(A\left( {a;{1 \over a}} \right)\) là :
\(y - {1 \over a}= - {1 \over {{a^2}}}\left( {x - a} \right)\) hay \(y = - {1 \over {{a^2}}}x + {2 \over a}\)
LG b
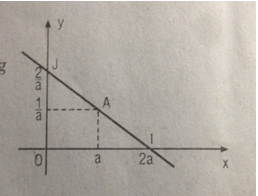
Giả sử (T) cắt trục Ox tại điểm I và cắt trục Oy tại điểm J. Chứng minh rằng A là trung điểm của đoạn thẳng IJ. Từ đó suy ra cách vẽ tiếp tuyến (T).
Lời giải chi tiết:
Tìm các giao điểm của (T) với hai trục tọa độ:
Cho x=0 thì \(y={2 \over a}\).
Cho y=0 thì x=2a.
Do đó \(I\left( {2a;0} \right);\,J\left( {0;{2 \over a}} \right)\)
Ta thấy:
\[\left\{ \begin{array}{l} \frac{{{x_I} + {x_J}}}{2} = \frac{{2a + 0}}{2} = a = {x_A}\\ \frac{{{y_I} + {y_J}}}{2} = \frac{{0 + \frac{2}{a}}}{2} = \frac{1}{a} = {y_A} \end{array} \right.\]
Nên \(A\left( {a;{1 \over a}} \right)\) là trung điểm của đoạn IJ.
Từ đó suy ra cách vẽ tiếp tuyến (T) chính là đường thẳng IJ.
Ta chỉ cần lấy hai điểm I, J có tọa độ như trên và nối lại sẽ được tiếp tuyến cần tìm.
LG c
Chứng minh rằng diện tích tam giác OIJ không phụ thuộc vào vị trí của điểm A.
Lời giải chi tiết:
Ta có: \[OI = \left| {2a} \right|,OJ = \left| {\frac{2}{a}} \right|\]
Diện tích tam giác OIJ là :
\(S = {1 \over 2}OI.OJ= {1 \over 2}\left| {2a.{2 \over a}} \right| = 2\) (đvdt)
Vì S không phụ thuộc vào a nên diện tích tam giác OIJ không phụ thuộc vào vị trí của điểm A ϵ (H)