Câu 31 trang 117 SGK Hình học 11 Nâng cao
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính khoảng cách giữa hai đường thẳng BC’ và CD’
Đề bài
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính khoảng cách giữa hai đường thẳng BC’ và CD’
Lời giải chi tiết
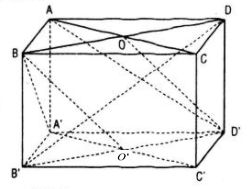
Gọi O, O’ lần lượt là tâm các hình vuông ABCD, A’B’C’D’ của hình lập phương ABCD.A’B’C’D’ cạnh a.
* Ta chứng minh B’D ⊥ (BA’C) và B’D ⊥ (ACD’)
Ta có: \(\left\{ {\matrix{ {A'C' \bot B'D'} \cr {A'C' \bot BB'} \cr } } \right. \Rightarrow A'C' \bot \left( {BB'D'D} \right)\)
Mà B’D ⊂ (BB’D’D) nên B’D ⊥ A’C’ (1)
Tương tự \(\left\{ {\matrix{ {AB' \bot A'B} \cr {A'B \bot B'C'} \cr } } \right. \Rightarrow A'B \bot \left( {AB'C'D} \right)\)
Mà B’D ⊂ (AB’C’D) nên B’D ⊥ A’B (2)
Từ (1) và (2) suy ra B’D ⊥ (BA’C’)
Tương tự ta cũng chứng minh được B’D ⊥ (ACD’)
* Hai mặt phẳng (BA’C’) và (ACD’) song song với nhau, vuông góc với đoạn B’D và chia B’D thành 3 phần bằng nhau (xét hình bình hành BB’DD’ và BO // D’O')
Do đó khoảng cách giữa mp(BA’C) và mp(ACD’) là \({{B'D} \over 3} = {{a\sqrt 3 } \over 3}\)
* Khoảng cách giữa BC’ và CD’
Khoảng cách giữa hai đường thẳng chéo nhau BC’ và CD’ bằng khoảng cách giữa hai mặt phẳng song song : mp(BA’C’) và mp(ACD’).
Vậy khoảng cách đó là \({{a\sqrt 3 } \over 3}\)