Câu 44 trang 47 SGK Đại số và Giải tích 11 Nâng cao — Không quảng cáo

Xét hàm số \(y = f(x) = \sinπx\).

LG a

Chứng minh rằng với mỗi số nguyên chẵn \(m\) ta có \(f(x + m) = f(x)\) với mọi \(x\).

Lời giải chi tiết:

Đặt \(m = 2k, k \in\mathbb Z\). Ta có :

\(f(x + m) = \sinπ(x + m) \)

\(= \sin(πx + 2kπ) = \sinπx = f(x)\)

LG b

Lập bảng biến thiên của hàm số trên đoạn \([-1 ; 1]\).

Lời giải chi tiết:

Bảng biến thiên

LG c

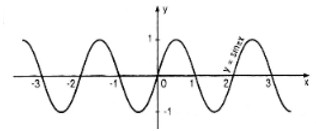
Vẽ đồ thị của hàm số đó.

Lời giải chi tiết:

Đồ thị