Câu 44 trang 167 SGK Đại số và Giải tích 11 Nâng cao — Không quảng cáo

Tìm các giới hạn sau :

LG a

$\mathop {\lim }\limits_{x \to - \infty } x\sqrt {{{2{x^3} + x} \over {{x^5} - {x^2} + 3}}}$

Lời giải chi tiết:

Với $x < 0$, ta có :

$x\sqrt {{{2{x^3} + x} \over {{x^5} - {x^2} + 3}}}$

$\eqalign{ &  = x\sqrt {\frac{{{x^3}\left( {2 + \frac{1}{{{x^2}}}} \right)}}{{{x^5}\left( {1 - \frac{1}{{{x^3}}} + \frac{3}{{{x^5}}}} \right)}}} \cr &= x\sqrt {\frac{{2 + \frac{1}{{{x^2}}}}}{{{x^2}\left( {1 - \frac{1}{{{x^3}}} + \frac{3}{{{x^5}}}} \right)}}}   \cr & = x.\frac{1}{{\left| x \right|}}.\sqrt {\frac{{2 + \frac{1}{{{x^2}}}}}{{1 - \frac{1}{{{x^3}}} + \frac{3}{{{x^5}}}}}}  \cr &  = x.\frac{1}{{ - x}}.\sqrt {\frac{{2 + \frac{1}{{{x^2}}}}}{{1 - \frac{1}{{{x^3}}} + \frac{3}{{{x^5}}}}}} \cr &= - \sqrt {{{2 + {1 \over {{x^2}}}} \over {1 - {1 \over {{x^3}}} + {1 \over {{x^5}}}}}} \cr}$

Do đó :  $\mathop {\lim }\limits_{x \to - \infty } x\sqrt {{{2{x^3} + x} \over {{x^5} - {x^2} + 3}}} = - \sqrt 2$

LG b

$\mathop {\lim }\limits_{x \to - \infty } {{\left| x \right| + \sqrt {{x^2} + x} } \over {x + 10}}$

Phương pháp giải:

Đưa $x^2$ ra ngoài dấu căn, chú ý dấu của x.

Lời giải chi tiết:

$\eqalign{ & \mathop {\lim }\limits_{x \to - \infty } {{\left| x \right|+\sqrt {{x^2} + x} } \over {x + 10}}\cr & = \mathop {\lim }\limits_{x \to  - \infty } \frac{{\left| x \right| + \sqrt {{x^2}\left( {1 + \frac{1}{x}} \right)} }}{{x + 10}}\cr & = \mathop {\lim }\limits_{x \to - \infty } {{\left| x \right| + \left| x \right|\sqrt {1 + {1 \over x}} } \over {x + 10}} \cr & = \mathop {\lim }\limits_{x \to - \infty } {{ - x - x\sqrt {1 + {1 \over x}} } \over {x + 10}} \cr &= \mathop {\lim }\limits_{x \to - \infty } {{ - 1 - \sqrt {1 + {1 \over x}} } \over {1 + {{10} \over x}}} \cr & = \frac{{ - 1 - \sqrt {1 + 0} }}{{1 + 0}}= - 2 \cr}$

LG c

$\mathop {\lim }\limits_{x \to + \infty } {{\sqrt {2{x^4} + {x^2} - 1} } \over {1 - 2x}}$

Lời giải chi tiết:

$\eqalign{ & \mathop {\lim }\limits_{x \to + \infty } {{\sqrt {2{x^4} + {x^2} - 1} } \over {1 - 2x}} \cr &= \mathop {\lim }\limits_{x \to + \infty } {{{x^2}\sqrt {2 + {1 \over {{x^2}}} - {1 \over {{x^4}}}} } \over {x\left( {{1 \over x} - 2} \right)}} \cr & = \mathop {\lim }\limits_{x \to + \infty } x{{\sqrt {2 + {1 \over {{x^2}}} - {1 \over {{x^4}}}} } \over {{1 \over x} - 2}} = - \infty \cr & \text{vì}\,\mathop {\lim }\limits_{x \to + \infty } x = + \infty \cr &\text{và}\,\mathop {\lim }\limits_{x \to + \infty } {{\sqrt {2 + {1 \over {{x^2}}} - {1 \over {{x^4}}}} } \over {{1 \over x} - 2}} = - {{\sqrt 2 } \over 2} < 0 \cr}$

Cách khác:

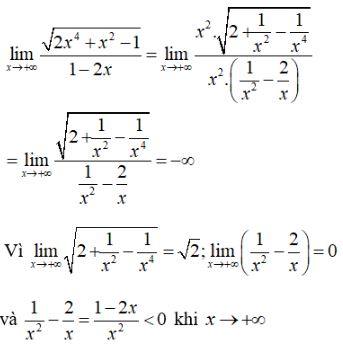
LG d

$\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {2{x^2} + 1} + x} \right)$

Phương pháp giải:

Nhân và chia với biểu thức $\left( {\sqrt {2{x^2} + 1} + x} \right)$

Lời giải chi tiết:

$\eqalign{ & \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {2{x^2} + 1} + x} \right)\cr & = \mathop {\lim }\limits_{x \to - \infty } {{2{x^2} + 1 - {x^2}} \over {\sqrt {2{x^2} + 1} - x}} \cr }$

$= \mathop {\lim }\limits_{x \to  - \infty } \dfrac{{{x^2} + 1}}{{\sqrt {{x^2}\left( {2 + \dfrac{1}{x^2}} \right)}  - x}}$

$= \mathop {\lim }\limits_{x \to  - \infty } x.\dfrac{{x + \dfrac{1}{x}}}{{\left| x \right|\sqrt {2 + \dfrac{1}{x^2}}  - x}}$

$= \mathop {\lim }\limits_{x \to  - \infty } x.\dfrac{{x + \dfrac{1}{x}}}{{ - x\sqrt {2 + \dfrac{1}{x^2}}  - x}}$

$= \mathop {\lim }\limits_{x \to  - \infty } x.\dfrac{{1 + \dfrac{1}{x^2}}}{{ - \sqrt {2 + \dfrac{1}{x^2}}  - 1}} =  + \infty$

Vì $\mathop {\lim }\limits_{x \to  - \infty } x =  - \infty$ và $\mathop {\lim }\limits_{x \to  - \infty } \dfrac{{1 + \dfrac{1}{x^2}}}{{ - \sqrt {2 + \dfrac{1}{x}}  - 1}} = \dfrac{1}{{ - \sqrt 2  - 1}} < 0$