Câu 8 trang 35 SGK Hình học 11 Nâng cao
Cho đường tròn (O) có đường kính AB.
Đề bài
Cho đường tròn (O) có đường kính AB. Gọi C là điểm đối xứng với A và B và PQ là đường kính thay đổi của (O) khác đường kính AB. Đường thẳng CQ cắt PA và PB lần lượt tại M và N
a. Chứng minh rằng Q là trung điểm của CM, N là trung điểm của CQ.
b. Tìm quỹ tích các điểm M và N khi đường kính PQ thay đổi
Lời giải chi tiết
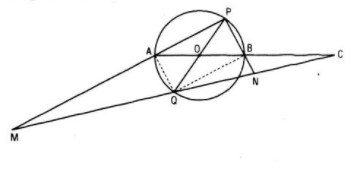
a. Ta có QB // AP (vì cùng vuông góc với PB) và B là trung điểm của AC nên Q là trung điểm của CM
Ta có AQ // BN (vì cùng vuông góc với AP) và B là trung điểm của AC nên N là trung điểm của CQ
b. Theo câu a) ta có \(\overrightarrow {CM} = 2\overrightarrow {CQ} \) nên phép vị tự V tâm C tỉ số 2 biến Q thành M
Vì Q chạy trên đường tròn (O) (trừ hai điểm A, B) nên quỹ tích M là ảnh của đường tròn đó qua phép vị tự V tâm C tỉ số 2 (trừ ảnh của A, B)
Tương tự, ta có \(\overrightarrow {CN} = {1 \over 2}\overrightarrow {CQ} \) nên quỹ tích N là ảnh của đường tròn (O) qua phép vị tự V tâm C, tỉ số \({1 \over 2}\) (trừ ảnh của A, B)