Đề kiểm tra 15 phút - Đề số 2 - Bài 2 - Chương 1 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 2 - Chương 1 - Hình học 9
Đề bài
Bài 1 . Cho \(∆ABC\) vuông tại A. Chứng minh rằng : \({{AC} \over {AB}} = {{\sin B} \over {\sin C}}\)
Bài 2 . Dựng góc nhọn \(α\) biết \(\sinα = 0,5\) (Vẽ hình và nêu cách dựng)
Phương pháp giải - Xem chi tiết
Sử dụng:
Cho tam giác ABC vuông tại A, khi đó
\(\sin B=\dfrac{AC}{BC}( = \dfrac{{cạnh\,đối}}{{cạnh\,huyền}})\)
\(\sin C=\dfrac{AB}{BC}\)
Lời giải chi tiết
Bài 1.
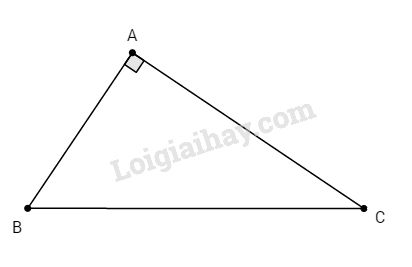
\(\sin B = {{AC} \over {BC}};\,{\mathop{\rm sinC}\nolimits} = {{AB} \over {BC}}\)
Do đó: \({{\sin B} \over {\sin C}} = {{AC} \over {BC}}:{{AB} \over {BC}} = {{AC} \over {AB}}\)
Bài 2. \(\sin \alpha = 0,5 = {1 \over 2}\)
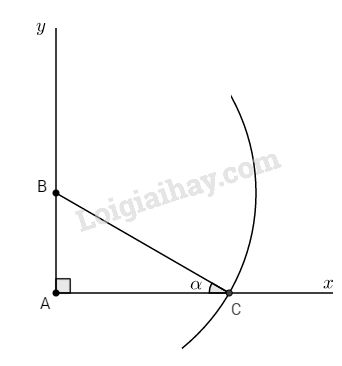
Cách dựng:
- Dựng góc vuông \(xAy\).
- B thuộc tia Ay sao cho \(AB = 1\)
- Dựng cung tròn tâm B bán kính 2.
- Lấy C là giao điểm của \((B; 2)\) và tia Ax.
- Nối B với C.
Khi đó \(\widehat {ACB} = \alpha \) là góc cần dựng.
Chứng minh:
Xét tam giác ABC vuông tại A có \(\sin \alpha=\sin C\)\(=\dfrac{AB}{BC} = {1 \over 2}=0,5\)