Đề kiểm tra 15 phút - Đề số 5 - Bài 1 - Chương 2 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 5 - Bài 1 - Chương 2 - Hình học 9
Đề bài
Cho hình vuông ABCD. Trên cạnh AB lấy điểm M, trên cạnh AD lấy điểm N sao cho \(AM = AN\). Từ A kẻ AH vuông góc với DM (H thuộc DM) và AH cắt BC tại P. Chứng minh rằng năm điểm C, D, N, H, P thuộc cùng một đường tròn.
Phương pháp giải - Xem chi tiết
Sử dụng:
Để chứng minh 5 điểm cùng thuộc một đường tròn, ta chứng minh 5 điểm đó cùng cách đều một điểm cố định
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Lời giải chi tiết
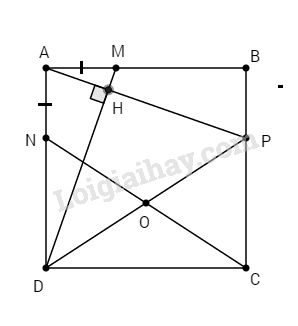
Ta có: \(AH ⊥ DM\) (gt)
nên \(\widehat {MAH} = \widehat {MDA}\) (cùng phụ với \(\widehat {AMD}\) )
Xét hai tam giác vuông ABP và DAM có:
\(AB = AD \;(gt)\)
\(\widehat {MAH} = \widehat {MDA}\) (cmt)
Do đó: ∆ABP = ∆DAM (g.c.g)
\(⇒ BP = AM\), mà \(AM = AN\; (gt)\)
\(⇒ BP = AN\), mà \(BC = AD (gt)\)
\(⇒ PC = ND\)
Vậy PCDN là hình chữ nhật. Gọi O là giao điểm của hai đường chéo PD và CN, ta có: \(OP = OC = OD = ON\), chứng tỏ bốn điểm P, C, D, N thuộc cùng một đường tròn.
Mặt khác: ∆PHD vuông tại H có OH là đường trung tuyến nên
\(OH = {1 \over 2}PD\)
Vậy: \(OH = OP = OD = OC = ON.\)
Năm điểm C, D, N, H, P thuộc cùng một đường tròn.