Đề kiểm tra 15 phút - Đề số 5 - Bài 2 - Chương 1 - Hình học 9 — Không quảng cáo

Đề bài

Bài 1 . Dựng góc nhọn $α$ biết $\tan \alpha  = {4 \over 3}$ (vẽ hình và nêu cách dựng).

Bài 2 . Cho $∆ABC$ vuông tại A, $AB = 6cm$ và $\widehat B = \alpha .$ Biết $\tan \alpha  = {5 \over {12}},$ hãy tính AC, BC.

LG bài 1

Phương pháp giải:

Sử dụng: $\tan \alpha  = \dfrac{{cạnh\, đối}}{{cạnh\,kề}}$

Lời giải chi tiết:

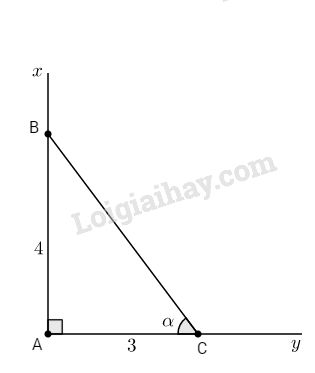
Cách dựng :

-  Dựng góc vuông $xAy$.

-  Lấy B thuộc tia Ax sao cho $AB = 4.$

-  Lấy C thuộc tia Ay sao cho  $AC = 3.$

-  Nối B với C.

Khi đó $\widehat {BCA} = \alpha$ góc cần dựng.

Chứng minh:

Xét tam giác ABC vuông tại A có $\tan\alpha =\dfrac{AB}{AC}=\dfrac{4}3$ thỏa mãn yêu cầu đề bài.

LG bài 2

Phương pháp giải:

Sử dụng: $\tan \alpha  = \dfrac{{cạnh\, đối}}{{cạnh\,kề}}$

Và định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Lời giải chi tiết:

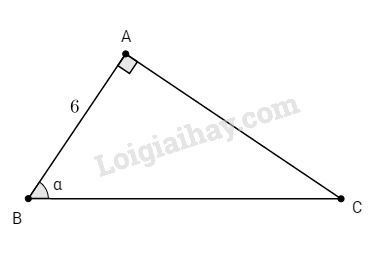
Xét tam giác ABC vuông tại A, ta có: $\tan \alpha  = {{AC} \over {AB}} = {5 \over {12}}$

hay ${{AC} \over 6} = {5 \over {12}} \Rightarrow AC = {{6.5} \over {12}} = 2,5\,\left( {cm} \right)$

Xét tam giác ABC vuông tại A, theo định lý Pytago ta có:

$BC = \sqrt {A{B^2} + A{C^2}}$$\;= \sqrt {{6^2} + {{\left( {2,5} \right)}^2}}  = 6,5\,\left( {cm} \right)$